Cho tam giác \[ABC\] cân tại \[A,{\rm{ }}AH\] là đường cao. Gọi \[M,{\rm{ }}N\] lần lượt là trung điểm của \[AB,{\rm{ }}AC\]. Gọi \[D,{\rm{ }}E\] lần lượt là điểm sao cho \[M\] là trung điểm của \[HD,{\rm{ }}N\] là trung điểm của \[HE.\]

a) \[BH = HC\].

b) Tứ giác \[AHBD\] là hình thoi.

c) Giao điểm của \[BE\] và \[CD\] là trung điểm của \[AH\].

d) \[2DH = 3HE\].

Xem lời giải

Câu hỏi trong đề: Đề cương ôn tập giữa kì 1 Toán 8 Kết nối tri thức cấu trúc mới có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án: a) Đ. b) S. c) Đ. d) S.

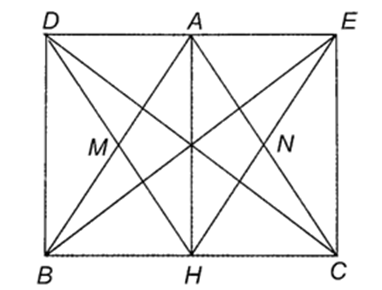
Cho tam giác ABC cân tại A, AH là đường cao. Gọi M, N lần lượt là trung điểm của AB, AC (ảnh 1)

⦁ Vì \[\Delta ABC\] cân tại \[A\] có \[AH\] là đường cao nên đồng thời là đường trung tuyến, do đó \[H\] là trung điểm của \[BC\], suy ra \[BH = HC\]. Do đó ý a) đúng.

⦁ Tứ giác \[AHBD\] có \[M\] là trung điểm của \[AB\] và \[HD\] nên là hình bình hành.

Do \[AH\] là đường cao của \[\Delta ABC\] nên \[AH \bot BC\], suy ra \[\widehat {AHB} = 90^\circ \].

Hình bình hành \[AHBD\] có \[\widehat {AHB} = 90^\circ \] nên \[AHBD\] là hình chữ nhật. Do đó ý b) sai.

⦁ Tương tự, tứ giác \[AHCE\] có \[N\] là trung điểm của \[AC\] và \[HE\] nên là hình bình hành.

Lại có \[\widehat {AHC} = 90^\circ \] nên \[AHCE\] là hình chữ nhật.

Vì \[ADBH,{\rm{ }}AECH\] là các hình chữ nhật nên \[AD = BH,{\rm{ }}AE = HC,{\rm{ }}AD{\rm{ // }}BC,{\rm{ }}AE{\rm{ // }}BC\].

Mà \[\Delta ABC\] cân tại \[A\] có \[AH\] là đường cao nên đồng thời là đường trung tuyến, do đó \[H\] là trung điểm của \[BC\], suy ra \[BH = HC\].

Từ đó, \[AD = BH = HC = AE\].

Tứ giác \[ADHC\] có: \[AD{\rm{ // }}HC,{\rm{ }}AD = HC\] nên \[ADHC\] là hình bình hành.

Tứ giác \[ABHE\] có: \[AE{\rm{ // }}BH,{\rm{ }}AE = BH\] nên \[ABHE\] là hình bình hành.

Vì \[ADHC\] và \[AEHB\] là hình bình hành nên \[CD\] và \[BE\] lần lượt cắt \[AH\] tại trung điểm của \[AH\].

Như vậy, giao điểm của \[BE\] và \[CD\] là trung điểm của \[AH\]. Do đó ý c) đúng.

⦁ Do \[AHBD,{\rm{ }}AHCE\] là các hình chữ nhật nên \[AB = DH,{\rm{ }}AC = HE\] (hai đường chéo bằng nhau).

Mà \[AB = AC\] (do \[\Delta ABC\] cân tại \[A\]) nên \[DH = HE\].

Do \[BCED\] là hình chữ nhật nên \[CD = BE\] (hai đường chéo bằng nhau).

Do đó ý d) sai.

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\].

Tính số đo góc \[\widehat {{C_1}}\] (đơn vị: độ).

Xem đáp án

Lời giải

Đáp số: 30.

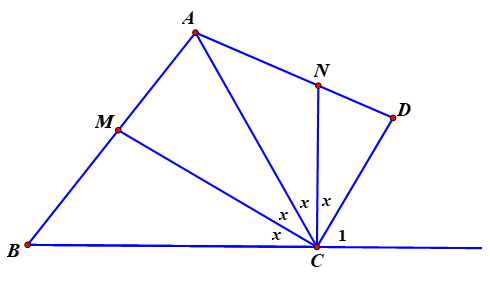
Xét tứ giác $ABCD$ có $\widehat {BAD} + \widehat B + \widehat {BCD} + \widehat D = 360^\circ $.

Suy ra $\frac{{7x}}{2} + 4x + 135^\circ = 360^\circ $ hay $\frac{{15x}}{2} = 225^\circ $ nên $x = 30^\circ .$

Câu 2

Giá trị của biểu thức \[A = {\left( {3x + 1} \right)^2} + {\left( {3x-1} \right)^2}-2\left( {3x-1} \right)\left( {3x + 1} \right)\] bằng

Xem đáp án

Lời giải

Đáp án: 4.

Ta có \[A = {\left( {3x + 1} \right)^2} + {\left( {3x-1} \right)^2}-2\left( {3x-1} \right)\left( {3x + 1} \right)\]

\[ = {\left[ {\left( {3x + 1} \right) - \left( {3x - 1} \right)} \right]^2}\]

\[ = {\left( {3x + 1 - 3x + 1} \right)^2} = {2^2} = 4\].

Vậy giá trị của biểu thức $A$ bằng 4.

Câu 3