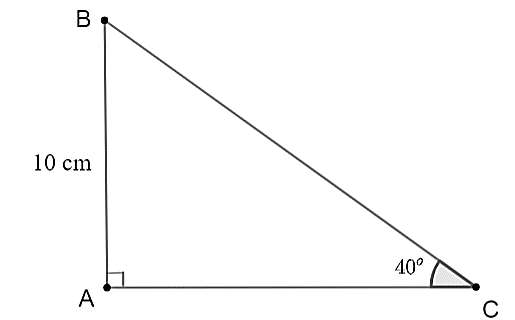
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 10\,\,{\rm{cm}},\,\,\widehat C = 40^\circ .\) Cạnh \(BC\) có độ dài gần nhất với kết quả nào dưới đây?

Hướng dẫn giải

Điểm trung bình của 40 học sinh là: \(\frac{{300}}{4} = 7,5\) (điểm).

Giả sử có một học sinh có điểm lớn hơn 30. Gọi điểm của học sinh đó là \[{a_k} > 30.\]

Điểm của các học sinh còn lại là \[{a_1},\,\,{a_2},\,\, \ldots ,\,\,{a_{k - 1}},\,\,{a_{k + 1}}\,\,,\,\, \ldots ,\,\,{a_{40}}.\]

Tổng điểm của các học sinh còn lại là: \[S = 300 - {a_k}.\]

Vì \[{a_k} > 30\] thì \[S < 300 - 30 = 270.\]

Số lượng học sinh còn lại là 39 nên trung bình điểm của các học sinh còn lại là:

\[M = \frac{S}{{39}} < \frac{{270}}{{39}} \approx 6,92.\]

Theo giả thiết, không có học sinh nào có điểm dưới 10.

Do đó, tổng điểm tối thiểu của 39 học sinh còn lại là: \[S\, \ge 10 \cdot 39 = 390.\]

Mà \[S < 270\] dẫn đến mâu thuẫn.

Vậy không có học sinh nào có điểm lớn hơn 30.

Hướng dẫn giải

Đáp án đúng là: B

Dễ dàng thấy rằng:

⦁ Giá trị \(x = 0\) không là nghiệm của phương trình \(\left( {x - 1} \right)\left( {x + 1} \right) = 0\).

⦁ Giá trị \(x = 0\) và \(x = - 1\) là nghiệm của phương trình \(x\left( {x + 1} \right) = 0\).

⦁ Giá trị \(x = - 1\) không là nghiệm của phương trình \(x = 0\) và phương trình \(x\left( {x - 1} \right) = 0\)

Vậy ta chọn phương án B.