Cho tam giác \(ABC\) có \(AB < AC,\) \(AI\) là đường cao và 3 điểm \(D,\,\,\,E,\,\,\,F\) theo thứ tự là trung điểm của các đoạn thẳng \(AB,\,\,\,AC,\,\,\,BC.\) Lấy \(J\) sao cho \(E\) là trung điểm \[IJ.\]
a) Tứ giác \[AICJ\] là hình gì? Vì sao?
b) Chứng minh tứ giác \(DEFI\) là hình thang cân.
c) \(EB\) và \(FD\) cắt nhau tại \(K.\) Chứng minh hai tứ giác \(ADKE\) và \(KECF\) có diện tích bằng nhau.
d) Tìm điều kiện của tam giác \(ABC\) để tứ giác \(BDEF\) là hình thoi, là hình vuông.
e) Giả sử \(DF \bot IE\). Chứng minh: \(DE + IF = AI\).
g) Gọi \(H\), \(G\) lần lượt là trung điểm của \(BI\) và \(IC\). Chứng minh: \(HE = DG\).
Cho tam giác \(ABC\) có \(AB < AC,\) \(AI\) là đường cao và 3 điểm \(D,\,\,\,E,\,\,\,F\) theo thứ tự là trung điểm của các đoạn thẳng \(AB,\,\,\,AC,\,\,\,BC.\) Lấy \(J\) sao cho \(E\) là trung điểm \[IJ.\]
a) Tứ giác \[AICJ\] là hình gì? Vì sao?
b) Chứng minh tứ giác \(DEFI\) là hình thang cân.
c) \(EB\) và \(FD\) cắt nhau tại \(K.\) Chứng minh hai tứ giác \(ADKE\) và \(KECF\) có diện tích bằng nhau.
d) Tìm điều kiện của tam giác \(ABC\) để tứ giác \(BDEF\) là hình thoi, là hình vuông.
e) Giả sử \(DF \bot IE\). Chứng minh: \(DE + IF = AI\).
g) Gọi \(H\), \(G\) lần lượt là trung điểm của \(BI\) và \(IC\). Chứng minh: \(HE = DG\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Tứ giác \[AICJ\] có hai đường chéo \(AC\) và \(IJ\) cắt nhau tại trung điểm của \[E\] của mỗi đường nên tứ giác \[AICJ\] là hình bình hành (dấu hiệu nhận biết)
Lại có \[\widehat {AIC} = 90^\circ \] (vì \(AI\) là đường cao của tam giác \(ABC)\)
Suy ra tứ giác \[AICJ\] là hình chữ nhật (dấu hiệu nhận biết).
b) Xét \(\Delta ABC\) có \(D,\,\,E\) lần lượt là trung điểm của \(AB,\,\,AC\) nên \(DE\) là đường trung bình của tam giác. Do đó \(DE = \frac{1}{2}BC\) và \(DE\,{\rm{//}}\,BC\) (tính chất đường trung bình).
Mà \(I,\,\,F \in BC\) nên \(DE\,{\rm{//}}\,IF.\)
Suy ra tứ giác \(DEFI\) là hình thang.
Xét tam giác \(AIC\) vuông tại \(I,\) có \(IE\) là đường trung tuyến ứng với cạnh huyền \(AC\) nên \(IE = AE = EC = \frac{1}{2}AC\) (tính chất đường trung tuyến ứng với cạnh huyền) (1)
Xét \(\Delta ABC\) có \(D,\,\,F\) lần lượt là trung điểm của \(AB,\,\,BC\) nên \(DF\) là đường trung bình của tam giác. Do đó \(DF\,{\rm{//}}\,AC\) và \(DF = \frac{1}{2}AC\) (tính chất đường trung bình) (2)
Từ (1) và (2) ta có \(IE = DF\left( { = \frac{1}{2}AC} \right).\)
Hình thang \(DEFI\) có hai đường chéo \(IE = DF\) nên \(DEFI\) là hình thang cân.
c) Vì \(F\) là trung điểm của \(BC\) nên \(BF = FC = \frac{1}{2}BC\).
Mà \(DE = \frac{1}{2}BC\) (chứng minh ở câu b)
Suy ra \(DE = BF.\)
Xét tứ giác \(BDEF\) có \(DE\,{\rm{//}}\,BF\) (do \(DE\,{\rm{//}}\,BC)\) và \(DE = BF\) nên \(BDEF\) là hình bình hành.
Do đó hai đường chéo \(EB\) và \(FD\) cắt nhau tại trung điểm của mỗi đường.
Suy ra \(K\) là trung điểm của \(FD\). Do đó \(DK = KF.\)
Ta có \(DF\,{\rm{//}}\,AC\) , mà \(K \in DF,\,\,E \in AC\) nên \(DK\,{\rm{//}}\,AE,\,\,KF\,{\rm{//}}\,EC\)
Do đó hai tứ giác \(ADKE\) và \(KECF\) là hình thang.
Từ \(K\) kẻ \(KM \bot AC.\) Khi đó \(KM\) là chiều cao của hình thang \(ADKE\) và \(KECF.\)
Ta có: \({S_{ADKE}} = \frac{1}{2} \cdot KM \cdot \left( {DK + AE} \right);\) \[{S_{KECF}} = \frac{1}{2} \cdot KM \cdot \left( {KF + EC} \right).\]
Mà \(DK = KF\) (chứng minh trên) và \(AE = EC\) (do \(E\) là trung điểm của \(AC)\)
Suy ra \({S_{ADKE}} = {S_{KECF}}\)
Vậy hai tứ giác \(ADKE\) và \(KECF\) có cùng diện tích.
d) Tứ giác \(BDEF\) có \(DE\,{\rm{//}}\,BF\) và \(DE = BF\,\,\left( { = \frac{1}{2}BC} \right)\) nên \(BDEF\) là hình bình hành.
⦁ Để hình bình hành \(BDEF\) là hình thoi thì \(BD = DE\).
Mà \(DE = \frac{1}{2}BC\) và \(BD = \frac{1}{2}AB\) nên suy ra cần điều kiện \(BC = AB\), tức là \(\Delta ABC\) cân tại \(B\).
⦁ Để hình bình hành \(BDEF\) là hình vuông thì \(BDEF\) là hình thoi và \(\widehat {DBF} = 90^\circ \), tức là \(\Delta ABC\) vuông cân tại \(B.\)
e) Vì \(D,\,\,F\) lần lượt là trung điểm của \(AB,\,\,BC\) nên \(DF\) là đường trung bình của tam giác \(ABC\), suy ra \(DF\,{\rm{//}}\,AC\).
Mà \(DF \bot IE\) nên \(IE \bot AC\).
Xét \(\Delta AIC\) vuông tại \(I\) có \(IE\) là đường trung tuyến đồng thời là đường cao nên \(\Delta AIC\) cân tại \(I\).
Do đó \(AI = IC = IF + FC.\)
Vì \(DE = \frac{1}{2}BC\) và \(FC = \frac{1}{2}BC\) nên \(DE = FC.\)
Khi đó, \(AI = IF + DE.\)
g) Xét \(\Delta AIB\) có \(D,\,\,H\) lần lượt là đường điểm của \(AB,\,\,BI\) nên \(DH\) là đường trung bình của tam giác, do đó \(DH\,{\rm{//}}\,AI\) và \(DH = \frac{1}{2}AI\). (3)
Tương tự, ta có \(EG\,{\rm{//}}\,AI\) và \(EG = \frac{1}{2}AI\). (4)
Từ (3), (4) ta có \(DH\,{\rm{//}}\,EG\) và \(DH = EG\).
Khi đó, tứ giác \(DHGE\) là hình bình hành.
Lại có \(DH\,{\rm{//}}\,AI,\,\,AI \bot BC\) nên \(DH \bot BC\), do đó hình bình hành \(DHGE\) là hình chữ nhật.
Suy ra \(HE = DG.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
![Tìm độ dài \[x,{\rm{ }}y\] trong mỗi trường hợp sau (làm tròn kết quả đến hàng phần mười): (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/screenshot-3568-1758353173.png)
Lời giải
Hướng dẫn giải
|
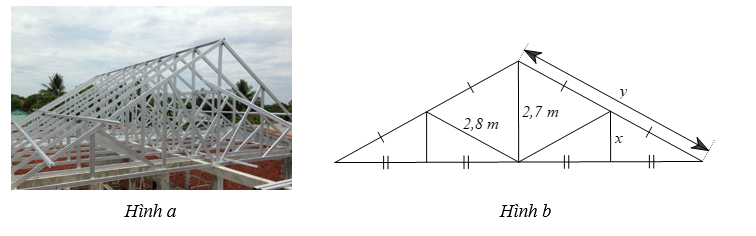
Ta có \(MB = AB - AM = 7 - 2 = 5.\) Tam giác \(ABC\) có \(MN\,{\rm{//}}\,AB,\) theo định lí Thalès ta có: \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) hay \(\frac{2}{5} = \frac{x}{6},\) suy ra \(x = \frac{{2 \cdot 6}}{5} = 2,4.\) Vậy \(x = 2,4.\) |
Hình 1 |
|
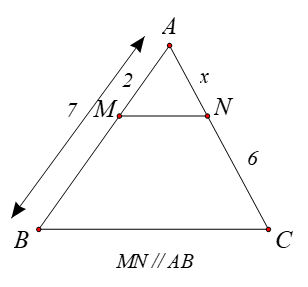
⦁ Hình 2: Ta có: \[EF \bot MN,\,\,NP \bot MN\] nên \[EF\,{\rm{//}}\,NP.\] \(MP = MF + FP = 5 + 15 = 20.\) Tam giác \[MNP\] có \[EF\,{\rm{//}}\,NP,\] theo định lí Thalès ta có: \[\frac{{ME}}{{MN}} = \frac{{MF}}{{MP}}\] hay \(\frac{3}{y} = \frac{5}{{20}},\) suy ra \(y = \frac{{3 \cdot 20}}{5} = 12.\) Vậy \(y = 12.\) |
Hình 2 |
|
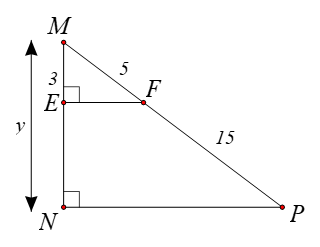
Tam giác \[ABC\] có \[M,\,\,N\] lần lượt là trung điểm của \[AB\] và \[AC\] nên \[MN\] là đường trung bình của tam giác. Do đó \[MN = \frac{1}{2}BC = \frac{1}{2} \cdot 15 = 7,5\,\,\left( {{\rm{cm}}} \right).\] Vậy \[x = 7,5\,\,{\rm{cm}}.\] |
Hình 3 |
|
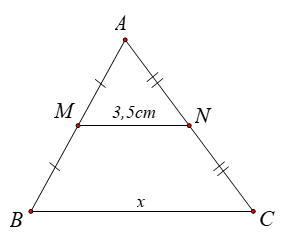
Tam giác \[ABC\] có \[M,\,\,N\] lần lượt là trung điểm của \[AB\] và \[AC\] nên \[MN\] là đường trung bình của tam giác. Do đó \[MN = \frac{1}{2}BC.\] Suy ra \[x = BC = 2MN = 2 \cdot 3,5 = 7\left( {{\rm{cm}}} \right).\] Vậy \(x = 7{\rm{\;cm}}.\) |
Hình 4 |
|
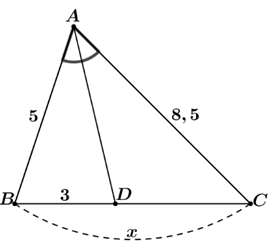
⦁ Hình 5: Xét tam giác \[ABC\] có \[AD\] là phân giác trong góc \[\widehat {BAC}\] (do \[\widehat {BAD} = \widehat {CAD}),\] nên \(\frac{{AB}}{{AC}} = \frac{{DB}}{{DC}},\) hay \[\frac{5}{{8,5}} = \frac{3}{{DC}}\] Suy ra \[DC = \frac{{8,5 \cdot 3}}{5} = 5,1.\] Khi đó \(x = BC = DB + DC = 3 + 5,1 = 8,1.\) |
Hình 5 |
|
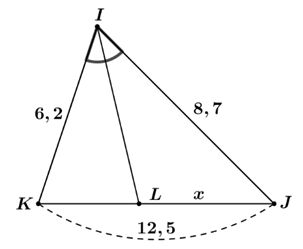
Xét tam giác \[IKJ\] có \[IL\] là phân giác trong góc \[\widehat {KIJ}\] (do \(\widehat {KIL} = \widehat {JIL}),\) nên \(\frac{{IK}}{{IJ}} = \frac{{LK}}{{LJ}}\) suy ra \[\frac{{LK}}{{IK}} = \frac{{LJ}}{{IJ}}\] hay \[\frac{{LK}}{{6,2}} = \frac{{LJ}}{{8,7}}\] Theo tính chất dãy tỉ số bằng nhau ta có: \[\frac{{LK}}{{6,2}} = \frac{{LJ}}{{8,7}} = \frac{{LK + LJ}}{{6,2 + 8,7}} = \frac{{KJ}}{{14,9}} = \frac{{12,5}}{{14,9}}.\] Suy ra \[LJ = \frac{{12,5}}{{14,9}} \cdot 8,7 \approx 7,3.\] |
Hình 6 |
Lời giải
|
a) Vì \(ABCD\) là hình thang có hai đáy \(AB\) và \(CD\) nên \(AB\,{\rm{//}}\,CD.\) Vì \(AB\,{\rm{//}}\,DM\) (do \(AB\,{\rm{//}}\,CD),\) nên theo hệ quả định lí Thalès ta có \(\frac{{AE}}{{EM}} = \frac{{AB}}{{DM}}.\) \(\left( 1 \right)\) Vì \(AB\,{\rm{//}}\,MC\) (do \(AB\,{\rm{//}}\,CD),\) nên theo hệ quả định lí |
|
![Chứng minh rằng \[EF\,{\rm{//}}\,AB.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/65-1758353408.png)
Thalès ta có \(\frac{{BF}}{{FM}} = \frac{{AB}}{{MC}}.\) \(\left( 2 \right)\)
Lại có \(M\) là trung điểm của \(CD\) nên \(DM = MC.\) \(\left( 3 \right)\)
Từ \(\left( 1 \right),\) \(\left( 2 \right)\) và \(\left( 3 \right)\) ta có \(\frac{{AE}}{{EM}} = \frac{{BF}}{{FM}},\) theo định lí Thalès đảo ta có \(EF\,{\rm{//}}\,AB.\)
b) Xét \(\Delta ADM\) có \(HE\,{\rm{//}}\,DM,\) theo hệ quả định lí Thalès ta có \(\frac{{HE}}{{DM}} = \frac{{AE}}{{AM}}.\)
Xét \(\Delta AMC\) có \(EF\,{\rm{//}}\,MC,\) theo hệ quả định lí Thalès ta có \[\frac{{EF}}{{MC}} = \frac{{AE}}{{AM}}.\]
Do đó \(\frac{{HE}}{{DM}} = \frac{{EF}}{{MC}},\) mà \(DM = MC\) nên \(HE = EF.\)
Chứng minh tương tự ta cũng có \(EF = FN.\) Suy ra \(HE = EF = FN.\)
c) Vì \(M\) là trung điểm của \(CD\) nên \(DM = MC = \frac{1}{2}CD = \frac{1}{2} \cdot 12 = 6{\rm{\;cm}}.\)
Theo câu a, ta có \(\frac{{AE}}{{EM}} = \frac{{AB}}{{DM}} = \frac{{7,5}}{6} = \frac{5}{4}.\) Suy ra \(\frac{{AE}}{5} = \frac{{EM}}{4}.\)
Theo tính chất của dãy tỉ số bằng nhau ta có: \(\frac{{AE}}{5} = \frac{{EM}}{4} = \frac{{AE + EM}}{{5 + 4}} = \frac{{AM}}{9}.\)
Do đó \(\frac{{AE}}{{AM}} = \frac{5}{9}.\)
Mà theo câu b, \[\frac{{HE}}{{DM}} = \frac{{AE}}{{AM}}\] nên \[\frac{{HE}}{{DM}} = \frac{5}{9}.\]
Suy ra \(HE = \frac{5}{9}DM = \frac{5}{9} \cdot 6 = \frac{{10}}{3}{\rm{\;cm}}.\)
Lại có \(HE = EF = FN\) (câu b) nên \(HN = 3HE = 3 \cdot \frac{{10}}{3} = 10{\rm{\;cm}}.\)
Vậy \(HN = 10{\rm{\;cm}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo