Cho hình vuông có chu vi 20 cm. Hỏi độ dài đường chéo của hình vuông đó bằng bao nhiêu? (Đơn vị: cm, kết quả làm tròn đến chữ số hàng phần mười)
Quảng cáo
Trả lời:
Đáp án: 7,1
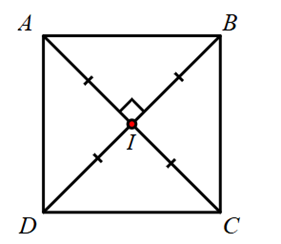
Giả sử hình vuông \(ABCD\) có chu vi bằng 20 cm.
Do đó, độ dài cạnh của hình vuông đó là: \(20:4 = 5{\rm{ }}\left( {{\rm{cm}}} \right)\).
Gọi giao điểm của hai đường chéo \(AC,BD\) là \(I.\)
Áp dụng định lý Pythagore vào tam giác \(AID,\) ta có:
\(A{I^2} + I{D^2} = A{D^2}\) hay \(2A{I^2} = {5^2}\) nên \(AI = \sqrt {\frac{{25}}{2}} {\rm{ }}\left( {{\rm{cm}}} \right)\).
Mà \(AC = 2AI = 2\sqrt {\frac{{25}}{2}} {\rm{ }}\left( {{\rm{cm}}} \right) \approx 7,1{\rm{ cm}}\).
Vậy độ dài đường chéo của hình vuông đó bằng 7,1 cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \(10\)
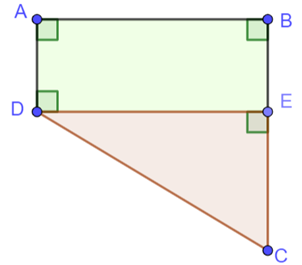
Tứ giác \(ABED\) có: \(\widehat A = \widehat B = \widehat {BED} = \widehat {EDA} = 90^\circ \) nên tứ giác \(ABED\) là hình chữ nhật.
Do đó, \(EB = AD = 4\;{\rm{m,}}\;AB = DE.\)
Ta có: \(EC = CB - BE = 10 - 4 = 6\;\left( {\rm{m}} \right).\)
Diện tích tam giác \(DEC\) vuông tại \(E\) bằng \(30\;{{\rm{m}}^2}\) nên
\(\frac{1}{2}EC \cdot DE = 30\) hay \(\frac{1}{2} \cdot 6 \cdot DE = 30\), do đó \(DE = 10\;{\rm{m}}.\)
Do đó, \(AB = DE = 10\;{\rm{m}}.\) Vậy \(AB = 10\;{\rm{m}}.\)
Lời giải
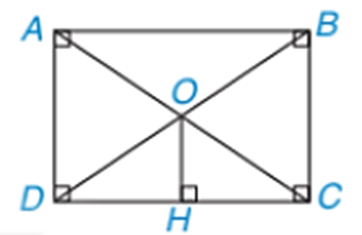
a) Đúng.
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(AC = BD.\)
b) Sai.
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(\widehat {DAB} = 90^\circ \) hay \(\widehat {DAO} + \widehat {OAB} = 90^\circ .\)
Theo đề bài: \(\widehat {DAO} = 2\widehat {OAB}\) nên \(\widehat {OAB} + 2\widehat {OAB} = 90^\circ .\) Suy ra \(3\widehat {OAB} = 90^\circ ,\) nên \(\widehat {OAB} = 30^\circ .\)
c) Sai.
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(OC = OD.\) Do đó, tam giác \(COD\) cân tại \(O.\)
Do đó, \(OH\) là đường cao đồng thời là đường trung tuyến của \(\Delta COD.\) Suy ra \(HC = \frac{1}{2}DC.\)
d) Đúng.
Vì \(\widehat {OAB} = 30^\circ \) nên \(\widehat {DAO} = 2\widehat {OAB} = 2 \cdot 30^\circ = 60^\circ .\)
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(OA = OD.\) Do đó, tam giác \(AOD\) cân tại \(O.\)
Mà \(\widehat {OAD} = 60^\circ \) nên tam giác \(AOD\) là tam giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.