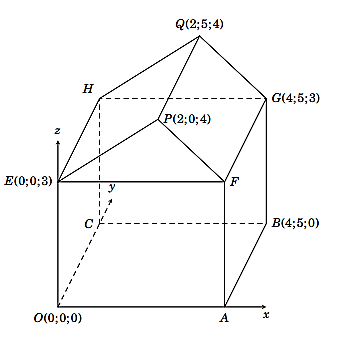
Hình minh họa sơ đồ một ngôi nhà trong hệ trục tọa độ $Oxyz$, trong đó nền nhà, bốn bức tường và hai mái nhà đều là hình chữ nhật.

$Tọa độ của các điểm $A\left( {5;0;0} \right)$. (ảnh 1)$

a) Tọa độ của các điểm $A\left( {5;0;0} \right)$.

b) Tọa độ của các điểm $H\left( {0;5;3} \right)$.

c) Góc nhị diện có cạnh là đường thẳng $FG$, hai mặt lần lượt là $\left( {FGQP} \right)$ và $\left( {FGHE} \right)$ gọi là góc dốc của mái nhà. Số đo của góc dốc của mái nhà bằng $26,6^\circ $ (làm tròn kết quả đến hàng phần mười của độ).

d) Chiều cao của ngôi nhà là 4.

Xem lời giải

Câu hỏi trong đề: Bài tập ôn tập Toán 12 Kết nối tri thức Chương 2 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Sai. Vì nền nhà là hình chữ nhật nên tứ giác $OABC$ là hình chữ nhật, suy ra ${x_A} = {x_B} = 4,{y_C} = {y_B} = $ 5. Do $A$ nằm trên trục $Ox$ nên tọa độ điểm $A$ là $\left( {4;0;0} \right)$.

b) Sai. Tường nhà là hình chữ nhật, suy ra ${y_H} = {y_C} = 5,{z_H} = {z_E} = 3$. Do $H$ nằm trên mặt phẳng $\left( {Oyz} \right)$ nên tọa độ điểm $H$ là $\left( {0;5;3} \right)$.

c) Sai. Để tính góc dốc của mái nhà, ta đi tính số đo góc nhị diện có cạnh là đường thẳng $FG$, hai mặt phẳng lần lượt là $\left( {FGQP} \right)$ và $\left( {FGHE} \right)$. Do mặt phẳng $\left( {Ozx} \right)$ vuông góc với hai mặt phẳng $\left( {FGQP} \right)$ và $\left( {FGHE} \right)$ nên góc $PFE$ là góc phẳng nhị diện ứng với góc nhị diện đó.

Ta có $\overrightarrow {FP} = \left( { - 2;0;1} \right),\overrightarrow {FE} = \left( { - 4;0;0} \right)$.

Suy ra ${\rm{cos}}\widehat {PFE} = {\rm{cos}}\left( {\overrightarrow {FP} ,\overrightarrow {FE} } \right) = \frac{{\overrightarrow {FP} \cdot \overrightarrow {FE} }}{{\left| {\overrightarrow {FP} \left| \cdot \right|\overrightarrow {FE} } \right|}} = \frac{{\left( { - 2} \right) \cdot \left( { - 4} \right) + 0 \cdot 0 + 1 \cdot 0}}{{\sqrt {{{( - 2)}^2} + {0^2} + {1^2}} \cdot \sqrt {{{( - 4)}^2} + {0^2} + {0^2}} }} = \frac{{2\sqrt 5 }}{5}$.

Do đó, $\widehat {PFE} \approx 26,6^\circ $. Vậy góc dốc của mái nhà khoảng $26,6^\circ $.

d) Sai. Chiều cao bằng cao độ của điểm $P$ suy ra $h = 4$.

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ thỏa mãn điều kiện $\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1$ và $\overrightarrow a .\overrightarrow b = 3.$ Độ dài vectơ $3\overrightarrow a + 5\overrightarrow b $ là

A. $5\sqrt 5 .$

B. $\sqrt {124} .$

C. 8.

D. 124.

Lời giải

Chọn B

${\left( {3\overrightarrow a + 5\overrightarrow b } \right)^2} = 9{\overrightarrow a ^2} + 30\overrightarrow a \overrightarrow b + 25{\overrightarrow b ^2}$ $ = 9 + 90 + 25 = 124$$ \Rightarrow \left| {3\overrightarrow a + 5\overrightarrow b } \right| = \sqrt {124} $.

Câu 2

Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm $A\left( {800;500;7} \right)$ đến điểm $B\left( {940;550;8} \right)$ trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo $D\left( {x;y;z} \right)$. Khi đó $x + y + z = ?$

$Khi đó $x + y + z = ?$ (ảnh 1)$

Xem đáp án

Lời giải

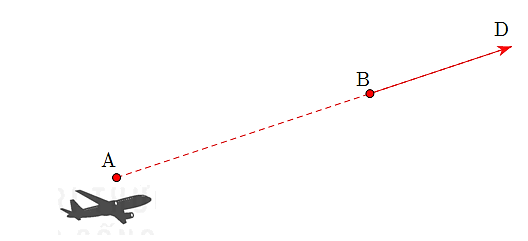
Gọi $D\left( {x;y;z} \right)$ là vị trí của máy bay sau 10 phút bay tiếp theo (tính từ thời điểm máy bay ở điểm $B$). Vì hướng của máy bay không đổi nên $\overrightarrow {AB} $ và $\overrightarrow {BD} $ cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ $A$ đến $B$ bằng thời gian bay từ \[B\] đến $D$ nên $AB = BD$.

Do đó, $\overrightarrow {BD} = \overrightarrow {AB} = \left( {140;50;1} \right)$.

Mặt khác: $\overrightarrow {BD} = \left( {x - 940;y - 550;z - 8} \right)$ nên $\left\{ {\begin{array}{*{20}{l}}{x - 940 = 140}\\{y - 550 = 50}\\{z - 8 = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1080}\\{y = 600}\\{z = 9}\end{array}} \right.} \right.$.

Vậy $D\left( {1080;600;9} \right)$. Vậy tọa độ của máy bay trong 10 phút tiếp theo là $\left( {1080;600;9} \right)$.

Suy ra $x + y + z = 1689$.

Đáp án: 1689.

Câu 3