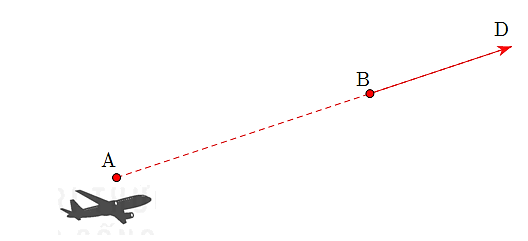
Trong không gian với hệ trục $Oxyz$ (đơn vị trên mỗi trục là 1 m), một flycam bay với vận tốc có độ lớn và hướng không đổi. Tại thời điểm $t = 0$, flycam ở vị trí $A\left( {1;\,2;\,3} \right)$ và sau 10 phút nó ở vị trí $B\left( {21;\,32;\,33} \right)$.

a) Flycam không bay qua vị trí \[D\left( {5;\,8;\,9} \right)\].

b) Vectơ vận tốc của flycam có tọa độ là $\overrightarrow v = \left( {20;\,30;\,30} \right)$.

c) Độ lớn của vận tốc flycam là $\sqrt {22} $ (m/phút).

d) Sau 15 phút vị trí flycam là $C\left( {31;\,47;\,48} \right)$.

Xem lời giải

Câu hỏi trong đề: Bài tập ôn tập Toán 12 Kết nối tri thức Chương 2 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

$Flycam không bay qua vị trí \[D\left( {5;\,8;\,9} \right)\]. (ảnh 1)$

a) Sai. $\overrightarrow {AB} = \left( {20;\,30;\,30} \right)$; $\overrightarrow {AD} = \left( {4;\,6;\,6} \right)$.

Ta có $\frac{{20}}{4} = \frac{{30}}{6} = \frac{{30}}{6}$.

Suy ra $\overrightarrow {AB} $, $\overrightarrow {AD} $ cùng phương.

$ \Rightarrow $ 3 điểm $A$, $B$, $D$ thẳng hàng.

Do đó flycam bay qua vị trí \[D\left( {5;\,8;\,9} \right)\].

b) Sai. Flycam ở vị trí $A\left( {1;\,2;\,3} \right)$ và sau 10 phút nó ở vị trí $B\left( {21;\,32;\,33} \right)$

$ \Rightarrow $ $\overrightarrow {AB} = 10\overrightarrow v $$ \Leftrightarrow \overrightarrow v = \frac{{\overrightarrow {AB} }}{{10}} = \left( {2;\,3;\,3} \right)$.

c) Đúng. Độ lớn của vận tốc flycam là $\left| {\overrightarrow v } \right| = \sqrt {{2^2} + {3^2} + {3^2}} = \sqrt {22} $(m/phút).

d) Đúng. Tại thời điểm $t = 0$, flycam ở vị trí $A$ và sau 15 phút flycam ở vị trí $C$.

Suy ra $\overrightarrow {AC} = 15\overrightarrow v $$ \Leftrightarrow \left( {{x_C} - 1;\,{y_C} - 2;\,{z_C} - 3} \right) = 15\left( {2;\,3;\,3} \right)$$ \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 31\\{y_C} = 47\\{z_C} = 48\end{array} \right.$.

Vậy $C\left( {31;\,47;\,48} \right)$.

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ thỏa mãn điều kiện $\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1$ và $\overrightarrow a .\overrightarrow b = 3.$ Độ dài vectơ $3\overrightarrow a + 5\overrightarrow b $ là

A. $5\sqrt 5 .$

B. $\sqrt {124} .$

C. 8.

D. 124.

Lời giải

Chọn B

${\left( {3\overrightarrow a + 5\overrightarrow b } \right)^2} = 9{\overrightarrow a ^2} + 30\overrightarrow a \overrightarrow b + 25{\overrightarrow b ^2}$ $ = 9 + 90 + 25 = 124$$ \Rightarrow \left| {3\overrightarrow a + 5\overrightarrow b } \right| = \sqrt {124} $.

Câu 2

Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm $A\left( {800;500;7} \right)$ đến điểm $B\left( {940;550;8} \right)$ trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo $D\left( {x;y;z} \right)$. Khi đó $x + y + z = ?$

$Khi đó $x + y + z = ?$ (ảnh 1)$

Xem đáp án

Lời giải

Gọi $D\left( {x;y;z} \right)$ là vị trí của máy bay sau 10 phút bay tiếp theo (tính từ thời điểm máy bay ở điểm $B$). Vì hướng của máy bay không đổi nên $\overrightarrow {AB} $ và $\overrightarrow {BD} $ cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ $A$ đến $B$ bằng thời gian bay từ \[B\] đến $D$ nên $AB = BD$.

Do đó, $\overrightarrow {BD} = \overrightarrow {AB} = \left( {140;50;1} \right)$.

Mặt khác: $\overrightarrow {BD} = \left( {x - 940;y - 550;z - 8} \right)$ nên $\left\{ {\begin{array}{*{20}{l}}{x - 940 = 140}\\{y - 550 = 50}\\{z - 8 = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1080}\\{y = 600}\\{z = 9}\end{array}} \right.} \right.$.

Vậy $D\left( {1080;600;9} \right)$. Vậy tọa độ của máy bay trong 10 phút tiếp theo là $\left( {1080;600;9} \right)$.

Suy ra $x + y + z = 1689$.

Đáp án: 1689.

Câu 3