Câu hỏi:

27/09/2025 272

Một kho chứa hàng có dạng hình lăng trụ đứng $ABFPE.DCGQH$ với \[ABFE\] là hình chữ nhật và $EFP$ là tam giác cân tại $P$. Gọi \[T\] là trung điểm của \[DC\]. Các kích thước của kho chứa lần lượt là $AB = 6$m;$AE = 5$m; $AD = 8$m; $QT = 7$m. Người ta mô hình hoá nhà kho bằng cách chọn hệ trục toạ độ có gốc toạ độ là điểm $O$ thuộc đoạn \[AD\] sao cho $OA = 2$m và các trục toạ độ tương ứng như hình vẽ dưới đây.

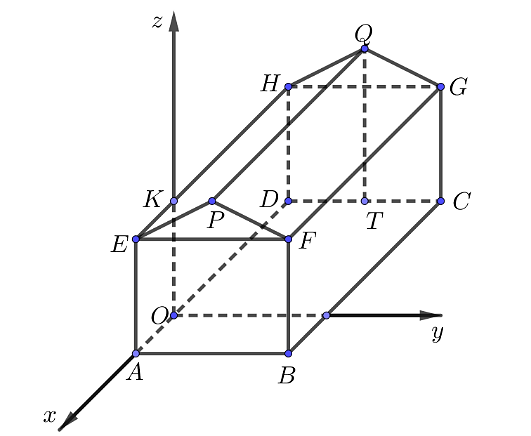
$a) Toạ độ điểm $Q$ là $\left( { - 6;3;5} \right)$. (ảnh 1)$

a) Toạ độ điểm $Q$ là $\left( { - 6;3;5} \right)$.

b) Vectơ $\overrightarrow {OC} $ có toạ độ là $\left( { - 6;6;0} \right)$.

c) Người ta muốn lắp camera quan sát trong nhà kho tại vị trí trung điểm của $FG$ và đầu thu dữ liệu đặt tại vị trí $O$. Người ta thiết kế đường dây cáp nối từ $O$ đến $K$ sau đó nối thẳng đến camera. Độ dài đoạn cáp nối tối thiểu bằng $5 + 2\sqrt {10} $m.

d) Mái nhà được lợp bằng tôn Hoa Sen, giá tiền mỗi mét vuông tôn là $130.000$ đồng. Số tiền cần bỏ ra để mua tôn lợp mái nhà là $3.750.000$ đồng (không kể hao phí do việc cắt và ghép các miếng tôn, làm tròn kết quả đến hàng nghìn).

Xem lời giải

Câu hỏi trong đề: Bài tập ôn tập Toán 12 Kết nối tri thức Chương 2 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

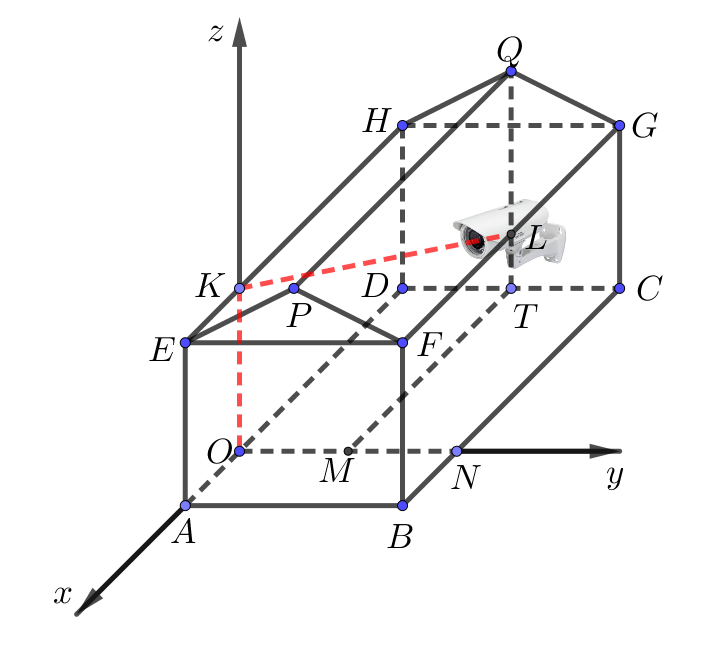
$a) Toạ độ điểm $Q$ là $\left( { - 6;3;5} \right)$. (ảnh 2)$

a) Sai. Kẻ $TM \bot Oy$, $CN \bot Oy$.

Vì $T$ là hình chiếu của $Q$ lên $\left( {Oxy} \right)$ nên

$\left\{ \begin{array}{l}{x_Q} = {x_T} = - OD = - \left( {AD - OA} \right) = - 6\\{y_Q} = {y_T} = OH = \frac{{AB}}{2} = 3\end{array} \right.$.

${z_Q} = QT = 7$

Suy ra $Q\left( { - 6;\,3;\,7} \right)$.

b) Đúng. Vì $C \in \left( {Oxy} \right)$ nên ${z_C} = 0$.

Ta có $\left\{ \begin{array}{l}{x_C} = - OD = - 6\\{y_C} = ON = AB = 6\end{array} \right.$. Suy ra $C\left( { - 6;\,6;\,0} \right)$. Vậy $\overrightarrow {OC} = \left( { - 6;\,6;\,0} \right)$.

c) Đúng Gọi $L$ là trung điểm của $FG$.

Ta có: ${z_K} = OK = AE = 5$.

Suy ra $K\left( {0;\,0;\,5} \right)$.

$ \Rightarrow OK = 5$.

$B$, $C$ lần lượt là hình chiếu của $F$, $G$ lên $\left( {Oxy} \right)$.

Suy ra $F\left( {2;\,6;\,5} \right)$, $G\left( { - 6;\,6;\,5} \right)$.

Mà $L$ là trung điểm của $FG$ nên $L\left( { - 2;\,6;\,5} \right)$$ \Rightarrow KL = 2\sqrt {10} $.

Vậy độ dài đoạn cáp tối thiểu từ $O$ đến $K$ sau đó nối thẳng đến camera là

$OK + KL = 5 + 2\sqrt {10} $ (m)

d) Sai. $FG = \sqrt {{{\left( { - 6 - 2} \right)}^2} + {{\left( {6 - 6} \right)}^2} + {{\left( {5 - 5} \right)}^2}} = 8$ (m) .

$GQ = \sqrt {{{\left( { - 6 + 6} \right)}^2} + {{\left( {3 - 6} \right)}^2} + {{\left( {7 - 5} \right)}^2}} = \sqrt {13} $ (m).

Suy ra ${S_{FGQP}} = FG \cdot GQ = 8\sqrt {13} $ $\left( {{{\rm{m}}^{\rm{2}}}} \right)$.

Diện tích lợp tôn mái nhà là $2{S_{FGQP}} = 16\sqrt {13} $ $\left( {{{\rm{m}}^{\rm{2}}}} \right)$.

Số tiền cần bỏ ra để mua tôn lợp mái nhà là

$16\sqrt {13} \cdot 130\,000 \approx 7\,500\,000$ (đồng).

Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai vectơ $\overrightarrow a $ và $\overrightarrow b $ thỏa mãn điều kiện $\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = 1$ và $\overrightarrow a .\overrightarrow b = 3.$ Độ dài vectơ $3\overrightarrow a + 5\overrightarrow b $ là

A. $5\sqrt 5 .$

B. $\sqrt {124} .$

C. 8.

D. 124.

Lời giải

Chọn B

${\left( {3\overrightarrow a + 5\overrightarrow b } \right)^2} = 9{\overrightarrow a ^2} + 30\overrightarrow a \overrightarrow b + 25{\overrightarrow b ^2}$ $ = 9 + 90 + 25 = 124$$ \Rightarrow \left| {3\overrightarrow a + 5\overrightarrow b } \right| = \sqrt {124} $.

Câu 2

Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo km), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm $A\left( {800;500;7} \right)$ đến điểm $B\left( {940;550;8} \right)$ trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 10 phút tiếp theo $D\left( {x;y;z} \right)$. Khi đó $x + y + z = ?$

$Khi đó $x + y + z = ?$ (ảnh 1)$

Xem đáp án

Lời giải

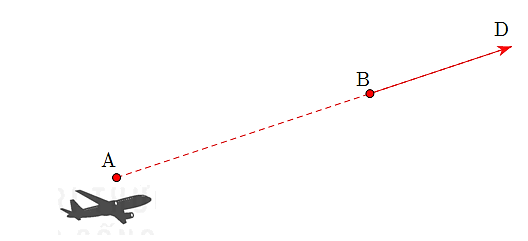
Gọi $D\left( {x;y;z} \right)$ là vị trí của máy bay sau 10 phút bay tiếp theo (tính từ thời điểm máy bay ở điểm $B$). Vì hướng của máy bay không đổi nên $\overrightarrow {AB} $ và $\overrightarrow {BD} $ cùng hướng. Do vận tốc máy bay không đổi và thời gian bay từ $A$ đến $B$ bằng thời gian bay từ \[B\] đến $D$ nên $AB = BD$.

Do đó, $\overrightarrow {BD} = \overrightarrow {AB} = \left( {140;50;1} \right)$.

Mặt khác: $\overrightarrow {BD} = \left( {x - 940;y - 550;z - 8} \right)$ nên $\left\{ {\begin{array}{*{20}{l}}{x - 940 = 140}\\{y - 550 = 50}\\{z - 8 = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1080}\\{y = 600}\\{z = 9}\end{array}} \right.} \right.$.

Vậy $D\left( {1080;600;9} \right)$. Vậy tọa độ của máy bay trong 10 phút tiếp theo là $\left( {1080;600;9} \right)$.

Suy ra $x + y + z = 1689$.

Đáp án: 1689.

Câu 3