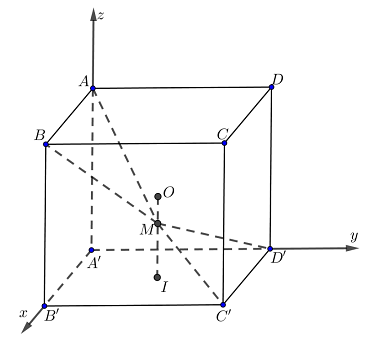
Cho hình lập phương \[ABCD.EFGH\]. Hãy xác định góc giữa cặp vectơ \(\overrightarrow {AB} \) và\(\overrightarrow {EG} \)?

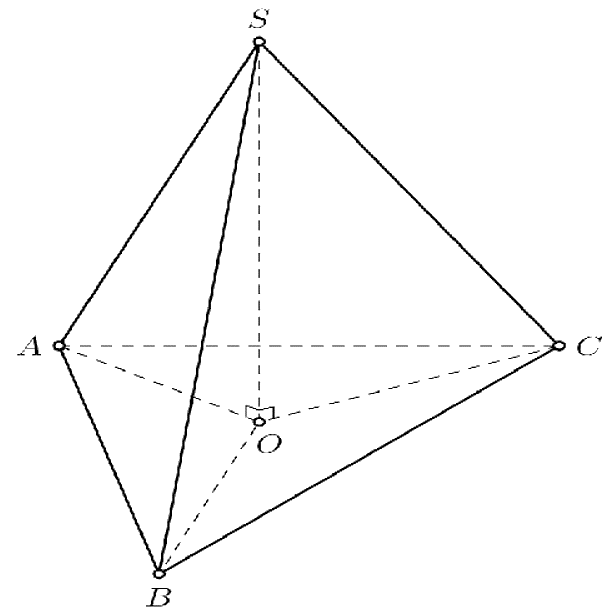
Biết ba sợi dây được thắt một đầu bên trên là điểm \(S\), ba sợi dây đỡ giá gỗ tại 3 điểm tạo thành tam giác đều \(ABC\),  độ dài sợi dây \(SA = SB = SC = 60\,\left( {{\rm{cm}}} \right)\), bán kính hình tròn\(OA = OB = OC = 20\,\left( {{\rm{cm}}} \right)\).

Ta có hình chóp tam giác đều \(S.ABC\), gọi \(O\)là tâm đường tròn ngoại tiếp tam giác \(ABC\).

\( \Rightarrow SO \bot (ABC)\) và \(SO = \sqrt {S{A^2} - O{A^2}}  = 40\sqrt 2 \left( {{\rm{cm}}} \right)\).

Gọi lực chịu đựng của mỗi sợi dây là \({T_1},\;T{}_2,{T_3}\)các lực này bằng nhau và không quá 15 N \( \Rightarrow {T_1} = {T_2} = {T_3} \le 15{\rm{N}}\)\( \Rightarrow \left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| \le 15\,{\rm{N}}\).

Lại có \(\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  = \overrightarrow {SO}  + \overrightarrow {OA}  + \overrightarrow {SO}  + \overrightarrow {OB}  + \overrightarrow {SO}  + \overrightarrow {OC}  = 3\overrightarrow {SO} \).

Gọi \(P\)là lực tác động lên miếng kê (là tổng lực của miếng giá gỗ hình tròn và lực của các chậu hoa) nên \(P = \left| {3\overrightarrow {SO} } \right| = 3SO\).

Vì \(P\)chia đều ra ba sợi dây

\( \Rightarrow \frac{P}{{3{T_1}}} = \frac{{3SO}}{{3SA}} = \frac{{SO}}{{SA}} = \frac{{40\sqrt 2 }}{{60}} = \frac{{2\sqrt 2 }}{3} \Leftrightarrow {T_1} = \frac{P}{{2\sqrt 2 }} \le 15{\rm{N}} \Leftrightarrow P \le 30\sqrt 2 {\rm{N}}\).

Suy ra trọng lượng của các chậu hoa là \({P_{hoa}} + {P_{go}} \le 30\sqrt 2 N \Leftrightarrow {P_{hoa}} \le \left( {30\sqrt 2  - 5} \right)N \approx 37,4{\rm{N}}\).

Vậy trọng lượng tối đa của các chậu hoa để dây treo không bị đứt là \(37,4{\rm{N}}\).

Đáp án: 37,4.

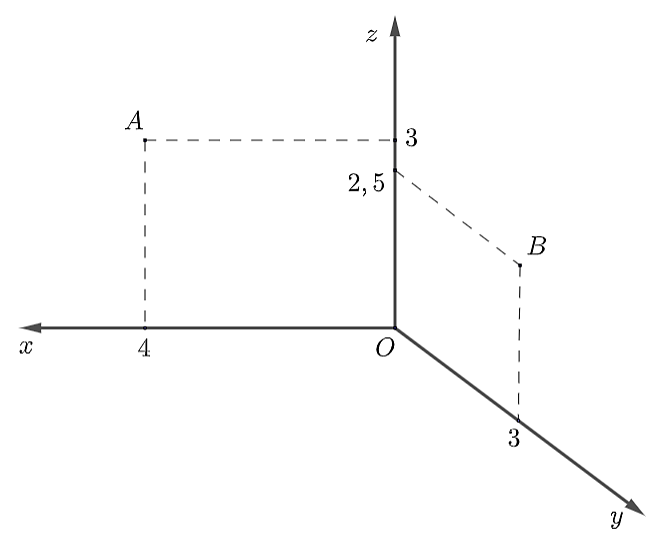
Vì \[M\] thuộc mặt phẳng sàn nhà có chiều dài 8 m, rộng 6 m nên \[M\left( {x;y;0} \right)\] với \[0 \le x \le 8,0 \le y \le 6\].

Cây quạt \[A\] treo chính giữa bức tường 8 m và cách trần 1 m, cây quạt \[B\] treo chính giữa bức tường 6 m và cách trần 1,5 m.

Suy ra \[A\left( {4;0;3} \right),B\left( {0,3,\frac{5}{2}} \right)\].

Ta có: \[\overrightarrow {MA}  = \left( {4 - x, - y,3} \right),\overrightarrow {MB}  = \left( { - x,3 - y,\frac{5}{2}} \right)\], \[\left| {\overrightarrow {MA}  - 2\overrightarrow {MB} } \right| = \sqrt {{{\left( {x + 4} \right)}^2} + {{\left( {y - 6} \right)}^2} + 4} \].

Để \[\left| {\overrightarrow {MA}  - 2\overrightarrow {MB} } \right|\] nhỏ nhất thì \[{\left( {x + 4} \right)^2} + {\left( {y - 6} \right)^2}\] nhỏ nhất.

Ta có: \[{\left( {x + 4} \right)^2} + {\left( {y - 6} \right)^2} \ge {\left( {0 + 4} \right)^2} + 0 = 16\].

Dấu bằng xảy ra khi \[x = 0,y = 6\].

Vậy \[{x^2} + {y^2} + {z^2} = {0^2} + {6^2} + {0^2} = 36\].

Đáp án: 36.