Phần 2. Trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Một tháp trung tâm kiểm soát không lưu ở sân bay cao 100 m sử dụng ra đa có phạm vi theo dõi 600 km được đặt trên đỉnh tháp. Chọn hệ trục tọa độ \[Oxyz\]có gốc \(O\) trùng với vị trí chân tháp, mặt phẳng \[\left( {Oxy} \right)\] trùng với mặt đất sao cho trục \[Ox\] hướng về phía tây, trục \(Oy\) hướng về phía nam, trục \(Oz\) hướng thẳng đứng lên phía trên (Hình dưới) (đơn vị độ dài trên mỗi trục là kilômét).

 

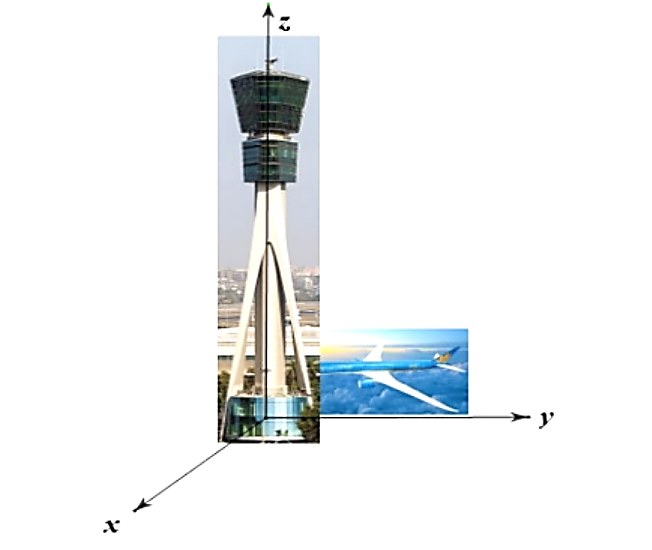
Một máy bay tại vị trí \(F\) cách mặt đất \(12{\rm{ km}}\), cách \(400{\rm{ km}}\) về phía tây và \(300{\rm{ km}}\) về phía bắc so với tháp trung tâm kiểm soát không lưu. Từ vị trí \(F\), máy bay bay với tốc độ \(900{\rm{ km/h}}\), theo hướng của vectơ \(\vec a = \left( {3;4;0} \right)\) sau một giờ đến vị trí \(A\). 

a) Tọa độ của ra đa đặt trên tháp \((0;0;0,1)\). 

b) Vị trí \(F\) nằm trong phạm vi kiểm soát của ra đa. 

c) Vị trí \(A\) có tọa độ \(A(940;420;0)\). 

d) Trong khoảng thời gian một giờ máy bay bay từ vị trí \(F\) đến vị trí \(A\), máy bay có không quá 21 phút bay trong phạm vi theo dõi của của ra đa. 

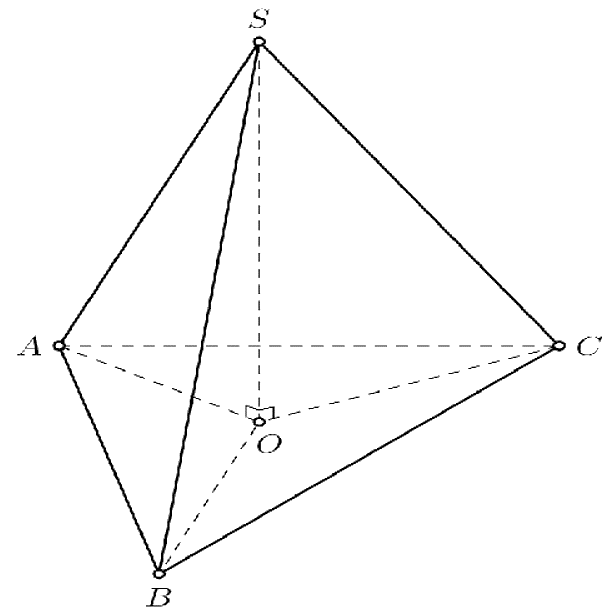
Biết ba sợi dây được thắt một đầu bên trên là điểm \(S\), ba sợi dây đỡ giá gỗ tại 3 điểm tạo thành tam giác đều \(ABC\),  độ dài sợi dây \(SA = SB = SC = 60\,\left( {{\rm{cm}}} \right)\), bán kính hình tròn\(OA = OB = OC = 20\,\left( {{\rm{cm}}} \right)\).

Ta có hình chóp tam giác đều \(S.ABC\), gọi \(O\)là tâm đường tròn ngoại tiếp tam giác \(ABC\).

\( \Rightarrow SO \bot (ABC)\) và \(SO = \sqrt {S{A^2} - O{A^2}}  = 40\sqrt 2 \left( {{\rm{cm}}} \right)\).

Gọi lực chịu đựng của mỗi sợi dây là \({T_1},\;T{}_2,{T_3}\)các lực này bằng nhau và không quá 15 N \( \Rightarrow {T_1} = {T_2} = {T_3} \le 15{\rm{N}}\)\( \Rightarrow \left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| \le 15\,{\rm{N}}\).

Lại có \(\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC}  = \overrightarrow {SO}  + \overrightarrow {OA}  + \overrightarrow {SO}  + \overrightarrow {OB}  + \overrightarrow {SO}  + \overrightarrow {OC}  = 3\overrightarrow {SO} \).

Gọi \(P\)là lực tác động lên miếng kê (là tổng lực của miếng giá gỗ hình tròn và lực của các chậu hoa) nên \(P = \left| {3\overrightarrow {SO} } \right| = 3SO\).

Vì \(P\)chia đều ra ba sợi dây

\( \Rightarrow \frac{P}{{3{T_1}}} = \frac{{3SO}}{{3SA}} = \frac{{SO}}{{SA}} = \frac{{40\sqrt 2 }}{{60}} = \frac{{2\sqrt 2 }}{3} \Leftrightarrow {T_1} = \frac{P}{{2\sqrt 2 }} \le 15{\rm{N}} \Leftrightarrow P \le 30\sqrt 2 {\rm{N}}\).

Suy ra trọng lượng của các chậu hoa là \({P_{hoa}} + {P_{go}} \le 30\sqrt 2 N \Leftrightarrow {P_{hoa}} \le \left( {30\sqrt 2  - 5} \right)N \approx 37,4{\rm{N}}\).

Vậy trọng lượng tối đa của các chậu hoa để dây treo không bị đứt là \(37,4{\rm{N}}\).

Đáp án: 37,4.

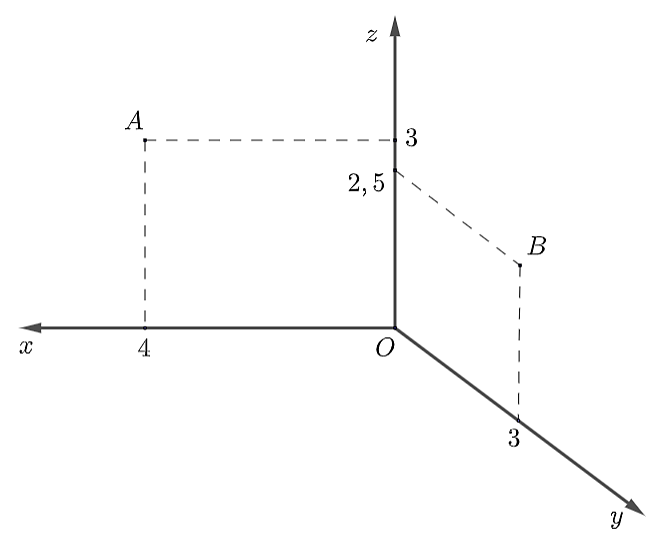
Vì \[M\] thuộc mặt phẳng sàn nhà có chiều dài 8 m, rộng 6 m nên \[M\left( {x;y;0} \right)\] với \[0 \le x \le 8,0 \le y \le 6\].

Cây quạt \[A\] treo chính giữa bức tường 8 m và cách trần 1 m, cây quạt \[B\] treo chính giữa bức tường 6 m và cách trần 1,5 m.

Suy ra \[A\left( {4;0;3} \right),B\left( {0,3,\frac{5}{2}} \right)\].

Ta có: \[\overrightarrow {MA}  = \left( {4 - x, - y,3} \right),\overrightarrow {MB}  = \left( { - x,3 - y,\frac{5}{2}} \right)\], \[\left| {\overrightarrow {MA}  - 2\overrightarrow {MB} } \right| = \sqrt {{{\left( {x + 4} \right)}^2} + {{\left( {y - 6} \right)}^2} + 4} \].

Để \[\left| {\overrightarrow {MA}  - 2\overrightarrow {MB} } \right|\] nhỏ nhất thì \[{\left( {x + 4} \right)^2} + {\left( {y - 6} \right)^2}\] nhỏ nhất.

Ta có: \[{\left( {x + 4} \right)^2} + {\left( {y - 6} \right)^2} \ge {\left( {0 + 4} \right)^2} + 0 = 16\].

Dấu bằng xảy ra khi \[x = 0,y = 6\].

Vậy \[{x^2} + {y^2} + {z^2} = {0^2} + {6^2} + {0^2} = 36\].

Đáp án: 36.