Tại 3 điểm A, B, C cố định trong chân không lần lượt đặt 3 điện tích điểm có giá trị lần lượt là \({q_1} = {6.10^{ - 6\,}}C,\,{q_2} = - {6.10^{ - 6\,}}C\) và \({q_3} = {3.10^{ - 6\,}}C.\)Biết AB = 3 cm, AC = 4 cm và \(BC = 5\,cm\). Lực tác dụng lên điện tích điểm đặt tại C có độ lớn bằng bao nhiêu N? Kết quả làm tròn đến ba chữ số có nghĩa.
Đáp án:
Tại 3 điểm A, B, C cố định trong chân không lần lượt đặt 3 điện tích điểm có giá trị lần lượt là \({q_1} = {6.10^{ - 6\,}}C,\,{q_2} = - {6.10^{ - 6\,}}C\) và \({q_3} = {3.10^{ - 6\,}}C.\)Biết AB = 3 cm, AC = 4 cm và \(BC = 5\,cm\). Lực tác dụng lên điện tích điểm đặt tại C có độ lớn bằng bao nhiêu N? Kết quả làm tròn đến ba chữ số có nghĩa.
|
Đáp án: |
|
|
|
|
Câu hỏi trong đề: Đề kiểm tra Vật Lí 11 Cánh diều Chủ đề 3 có đáp án !!
Quảng cáo
Trả lời:
|
Đáp án: |
6 |
2 |
, |
9 |
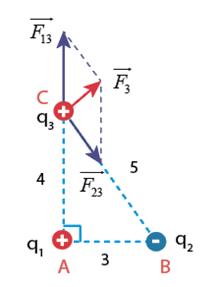
Vì \(A{B^2} + A{C^2} = B{C^2}\) nên \(\Delta ABC\) vuông tại A.
Lực do \({q_1}\) tác dụng vào \({q_3}\) có độ lớn là
\({F_{13}} = k\frac{{\left| {{q_1}{q_3}} \right|}}{{A{C^2}}} = {9.10^9}.\frac{{\left| {{{6.10}^{ - 6}}{{.3.10}^{ - 6}}} \right|}}{{0,{{04}^2}}} = 101,25\,N\)
Lực do \({q_2}\) tác dụng vào \({q_3}\) có độ lớn là
\({F_{23}} = k\frac{{\left| {{q_2}{q_3}} \right|}}{{B{C^2}}} = {9.10^9}.\frac{{\left| { - {{6.10}^{ - 6}}{{.3.10}^{ - 6}}} \right|}}{{0,{{05}^2}}} = 64,8\,N\)
\[{\rm{cos}}\widehat {ACB} = \frac{{AC}}{{BC}} = \frac{4}{5} \Rightarrow \widehat {ACB} = \arccos \frac{4}{5}\]
Lực tổng hợp tác dụng lên \({q_3}\) có:
+ phương, chiều như hình vẽ.
+ Độ lớn: \({F_3} = \sqrt {{F_{13}}^2 + {F_{23}}^2 + 2{F_{13}}{F_{23}}{\rm{cos(18}}{{\rm{0}}^0} - \widehat {ACB})} \approx 62,9\,N\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Đáp án: |
1 |
, |
8 |
|
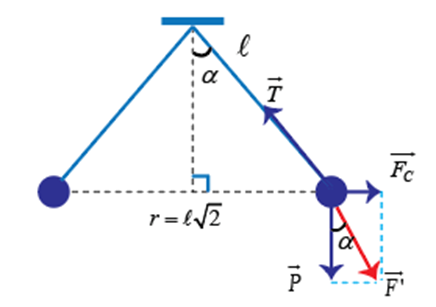
Khối lượng mỗi quả cầu: \({m_1} = {m_2} = m\)
Mỗi quả cầu chịu tác dụng của 3 lực:
+ Lực đẩy Culông \(\overrightarrow {{F_C}} \)
+ Trọng lực \(\overrightarrow P \)
+ Lực căng dây \(\overrightarrow T \)
Điều kiện cân bằng của quả cầu
\(\overrightarrow {{F_C}} + \overrightarrow P + \overrightarrow T = \overrightarrow 0 \Leftrightarrow \overrightarrow {F'} + \overrightarrow T = \overrightarrow 0 \Leftrightarrow \overrightarrow {F'} = - \overrightarrow T \)
Từ hình vẽ, ta có:
\(\tan \alpha = \frac{{{F_C}}}{P} \Leftrightarrow P\tan \alpha = {F_C} \Leftrightarrow mg\tan {45^0} = k\frac{{{q^2}}}{{{r^2}}}\) (với \(r = \ell \sqrt 2 \))
\( \Leftrightarrow m = \frac{{k{q^2}}}{{2g{\ell ^2}}} = \frac{{{{9.10}^9}{{.16.10}^{ - 14}}}}{{2.10.0,{2^2}}} = {18.10^{ - 4}}kg = 1,{8.10^{ - 3}}kg = 1,8g\)
Lời giải
|
|
Phát biểu |
Đúng |
Sai |
|
a |
Quỹ đạo chuyển động của electron là một nhánh parabol. |
Đ |
|
|
b |
Electron chuyển động lệch về bản kim loại phía dưới. |
|
S |
|
c |
Cường độ điện trường giữa hai bản kim loại là 1200 V/m. |
Đ |
|
|
d |
Độ lớn lực điện tác dụng lên electron là \(9,{6.10^{ - 17}}\,N\). |
|
S |
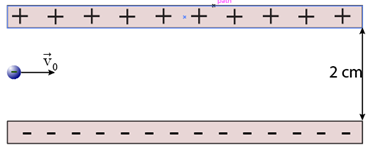
a) Quỹ đạo chuyển động của electron là một nhánh parabol.
b) Electron chuyển động lệch về bản kim loại phía trên.
c) \[E = \frac{U}{d} = \frac{{24}}{{0,02}} = 1200V/m\]
d) |F| = |q|E = 1,92.10-16 N.
Câu 3
hút nhau.
đẩy nhau.
có thể hút hoặc đẩy nhau.
không tương tác nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
đường thẳng song song với các đường sức điện.
đường thẳng vuông góc với các đường sức điện.
một phần của đường hypebol.
một phần của đường parabol
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
không phụ thuộc vào hình dạng đường đi của q.
phụ thuộc vào vị trí điểm đầu và điểm cuối của q.
phụ thuộc vào giá trị của điện tích q.
không phụ thuộc vào điện trường.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
điện tích và truyền tương tác giữa các điện tích.
dòng điện nhưng không truyền tương tác giữa các điện tích.
nam châm và truyền tương tác giữa các nam châm.
nam châm nhưng không truyền tương tác giữa các nam châm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.