Một khung dây dẫn có diện tích 40 cm$^2$ gồm 500 vòng dây, quay đều với tốc độ 3000 vòng/phút trong một từ trường đều có các đường sức từ vuông góc với trục quay của khung (trục quay nằm trong mặt phẳng khung dây dẫn) và có độ lớn cảm ứng từ bằng 0,02 T. Xem khung dây dẫn như một điện trở thuần có điện trở 25 $\Omega$. Nhiệt lượng tỏa ra trên khung dây dẫn trong 5 phút bằng bao nhiêu J (làm tròn kết quả đến chữ số hàng đơn vị)?
Một khung dây dẫn có diện tích 40 cm$^2$ gồm 500 vòng dây, quay đều với tốc độ 3000 vòng/phút trong một từ trường đều có các đường sức từ vuông góc với trục quay của khung (trục quay nằm trong mặt phẳng khung dây dẫn) và có độ lớn cảm ứng từ bằng 0,02 T. Xem khung dây dẫn như một điện trở thuần có điện trở 25 $\Omega$. Nhiệt lượng tỏa ra trên khung dây dẫn trong 5 phút bằng bao nhiêu J (làm tròn kết quả đến chữ số hàng đơn vị)?
Quảng cáo
Trả lời:
Nhiệt lượng tỏa ra trên khung dây trong 10 phút là:
\[
Q = I^2Rt = \frac{e_0^2}{2R}t = \frac{(NBS\omega)^2}{2R}t = \frac{(NBS2\pi f)^2}{2R}t
\]
\[
= \frac{\left(500.0,02.40.10^{-4}.2\pi.\frac{3000}{60}\right)^2}{2.25}t
= 5,60t \approx 947\ \mathrm{J}.
\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
Chu kì bán rã của chất phóng xạ này là 1,8 giờ. |
Đ |
|
|
b |
Tại thời điểm $t=0$ s, số hạt nhân có chứa trong mẫu chất phóng xạ đó xấp xỉ bằng $2,08.10^5$ hạt nhân.
|
|
S |
|
c |
Trong 3,6 giờ đầu, mẫu chất phóng xạ đó đã phát ra $1,56.10^5$ hạt positron. |
|
S |
|
d |
Kể từ thời điểm ban đầu, số hạt nhân chất phóng xạ còn lại trong mẫu sau 9 giờ bằng 1/64 số hạt nhân chất phóng xạ ban đầu. |
|
S |
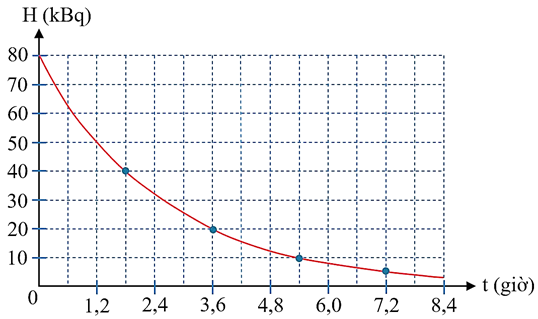
a) ĐÚNG
Dựa vào đồ thị ta xác định được khoảng thời gian để độ phóng xạ của mẫu chất giảm đi một nửa (hay một nửa số hạt nhân của mẫu phóng xạ phân rã) là 1,8 giờ.
Vậy chu kì bán rã của chất phóng xạ này là 1,8 giờ.
b) SAI
Tại thời điểm $t=0$ s, số hạt nhân có chứa trong mẫu chất phóng xạ đó:
\[
H_0 = \lambda N_0 \quad \Rightarrow \quad N_0 = \frac{T.H_0}{\ln 2} = \frac{1,8.3600.80.10^3}{\ln 2} \approx 7,48.10^8 \ \text{hạt nhân}.
\]
c) SAI
Số hạt positron được phát ra bằng số hạt nhân của mẫu chất phóng xạ đã phân rã. Trong 3,6 giờ đầu, số hạt positron đã được mẫu chất phóng xạ đó phát ra là:
\[
\Delta N = N_0\left(1-2^{-\tfrac{t}{T}}\right) = \frac{T.H_0}{\ln 2}\left(1-2^{-\tfrac{3,6}{1,8}}\right) = \frac{1,8.3600.80.10^3}{\ln 2}\left(1-2^{-2}\right) \approx 5,6.10^8 \ \text{hạt positron}.
\]
d) SAI
Sau 9 giờ kể từ thời điểm ban đầu, ta có:
\[
\frac{N_t}{N_0} = 2^{-\tfrac{t}{T}} = 2^{-\tfrac{9}{1,8}} = 2^{-5} = \frac{1}{32} \quad \Rightarrow \quad N_t = \frac{1}{32}N_0.
\]
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
Nhiệt lượng mà ấm điện tỏa ra trong 2 phút là $7,5 \cdot 10^4\ \mathrm{J}$. |
Đ |
|
|
b |
Hiệu suất của ấm điện xấp xỉ bằng 83,75%. |
Đ |
|
|
c |
Nếu hiệu suất của ấm điện luôn không đổi thì tiếp tục đun khoảng 180 phút nữa nước sẽ hóa hơi hoàn toàn. |
|
S |
|
d |
Tại thời điểm nước bắt đầu sôi, người ta ngắt điện của ấm và thả vào ấm một lượng nước đá ở 0 °C và có khối lượng bằng khối lượng nước trong ấm. Nếu bỏ qua sự trao đổi nhiệt với môi trường thì nhiệt độ của hỗn hợp khi xảy ra sự cân bằng nhiệt là 50 °C. |
|
S |
a)
\[
Q = I^2 R t = 2,5^2 \cdot 100 \cdot 2 \cdot 60 = 7,5 \cdot 10^4\ \mathrm{J}.
\]
b)
\[
H = \frac{Q_{thu}}{Q_{tỏa}} \cdot 100\%
= \frac{mc \Delta T}{I^2 R t} \cdot 100\%
= \frac{997 \cdot 1,5 \cdot 10^{-3} \cdot 4200 \cdot (100-25)}{2,5^2 \cdot 100 \cdot 15 \cdot 60} \cdot 100\%
\approx 83,75\%.
\]
c)
\[
Q_{cần} = mL = 1,5 \cdot 997 \cdot 10^{-3} \cdot 2,26 \cdot 10^6 \approx 3,39 \cdot 10^6\ \mathrm{J}.
\]
\[
t = \frac{Q_{cần}}{P \cdot H} \approx 108\ \text{phút}.
\]
d)
\[
Q_{tỏa} = Q_{thu} \quad \Rightarrow \quad mc(100 - t_{cb}) = \lambda m + mc(t_{cb} - 0).
\]
\[
4200(100 - t_{cb}) = 334 \cdot 10^3 + 4200 t_{cb} \quad \Rightarrow \quad t_{cb} \approx 10^\circ C.
\]
Câu 3
A. Sự nóng chảy.
B. Sự hóa hơi.
C. Sự ngưng kết.
D. Sự thăng hoa.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.