PHẦN 2: CÂU TRẮC NGHIỆM ĐÚNG SAI
Trong không gian cho hình lập phương \(ABCD.A'B'C'D'\) có độ dài cạnh là \(a\). Gọi \(O\)là giao điểm của \(BD\) và \(AC\).
a) Vectơ \[\overrightarrow {A'C} - \overrightarrow {A'A} = \overrightarrow {AB} + \overrightarrow {AD} \]
b) Vectơ \[\overrightarrow {BC'} = \overrightarrow {A'A} + \overrightarrow {B'C'} \].
c) Vectơ \[\overrightarrow {C'O} = \overrightarrow {C'A'} - \overrightarrow {OA'} \]
d) \(\overrightarrow {A'D} .\overrightarrow {A'B} = 0\)
PHẦN 2: CÂU TRẮC NGHIỆM ĐÚNG SAI
Trong không gian cho hình lập phương \(ABCD.A'B'C'D'\) có độ dài cạnh là \(a\). Gọi \(O\)là giao điểm của \(BD\) và \(AC\).
a) Vectơ \[\overrightarrow {A'C} - \overrightarrow {A'A} = \overrightarrow {AB} + \overrightarrow {AD} \]
b) Vectơ \[\overrightarrow {BC'} = \overrightarrow {A'A} + \overrightarrow {B'C'} \].
c) Vectơ \[\overrightarrow {C'O} = \overrightarrow {C'A'} - \overrightarrow {OA'} \]
d) \(\overrightarrow {A'D} .\overrightarrow {A'B} = 0\)
Câu hỏi trong đề: Đề kiểm tra Vectơ trong không gian (có lời giải) !!
Quảng cáo
Trả lời:
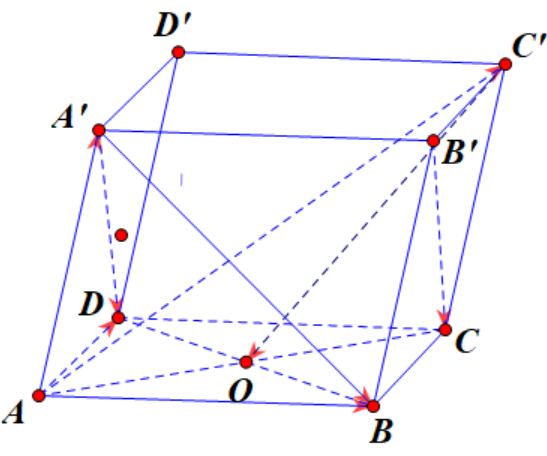
Ý a) Đúng: Vì \[\left\{ \begin{array}{l}\overrightarrow {A'C} - \overrightarrow {A'A} = \overrightarrow {AC} \\\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \end{array} \right. \Rightarrow \overrightarrow {A'C} - \overrightarrow {AA'} = \overrightarrow {AB} + \overrightarrow {AD} \]
Ý b) Sai: Vì \[\overrightarrow {BC'} = \overrightarrow {BB'} + \overrightarrow {B'C'} = \overrightarrow {AA'} + \overrightarrow {B'C'} \].
Ý c) Đúng: Vì \[\overrightarrow {C'O} = \overrightarrow {C'A'} + \overrightarrow {A'O} = \overrightarrow {C'A'} - \overrightarrow {OA'} \].
Ý d) Sai: Ta có: \(\overrightarrow {A'D} .\overrightarrow {A'B} = \left| {\overrightarrow {A'D} } \right|.\left| {\overrightarrow {A'B} } \right|.\cos \left( {\overrightarrow {A'D} ,\overrightarrow {A'B} } \right) = a\sqrt 2 .a\sqrt 2 .c{\rm{os}}60^\circ = {a^2}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)Đ b) S c) S d Đ
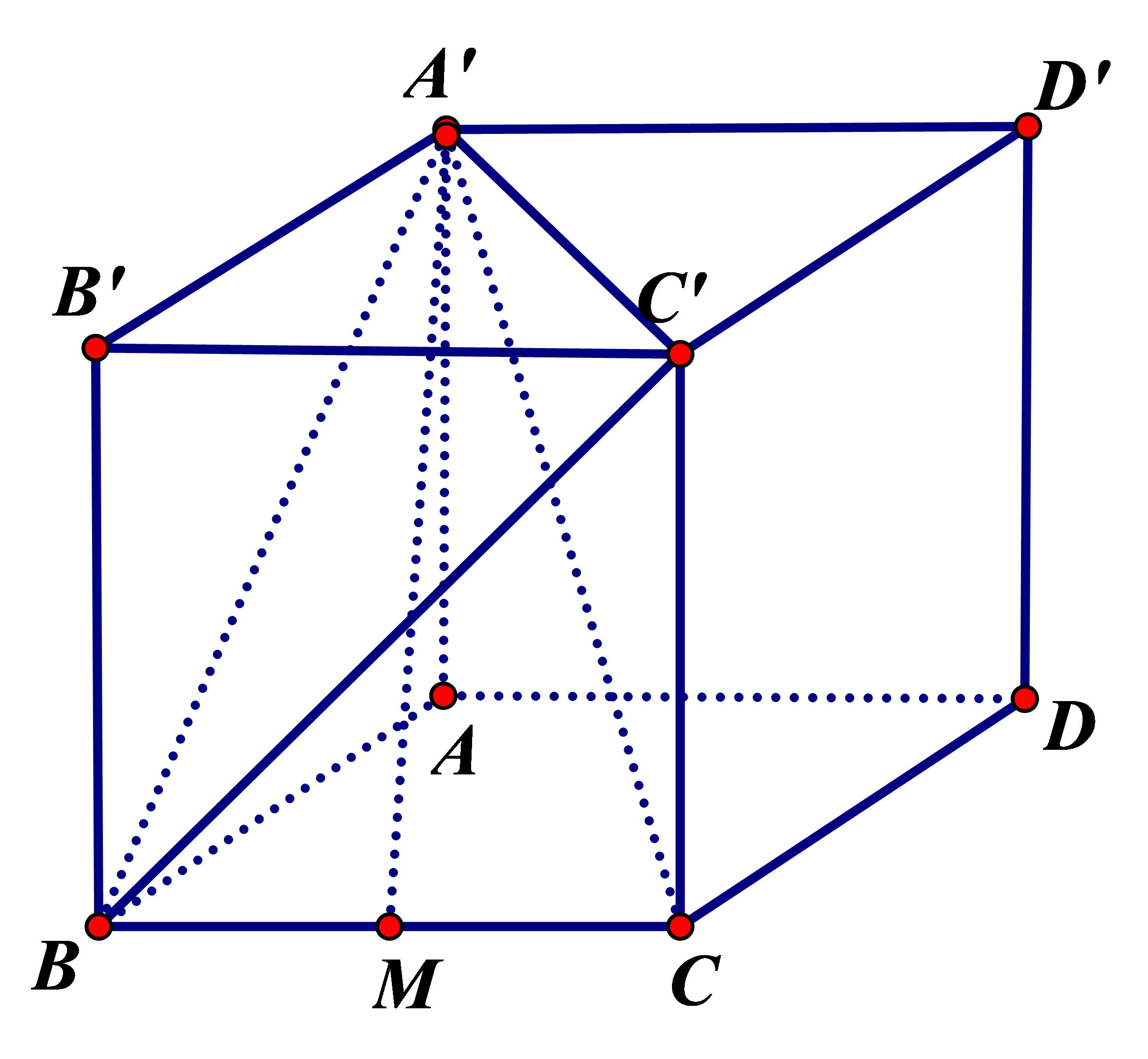
Theo quy tắc hình hộp ta có \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow x + \overrightarrow y + \overrightarrow z \).
b) Sai.
Theo quy tắc 3 điểm ta có \(\overrightarrow {A'B} = \overrightarrow {AB} - \overrightarrow {AA'} = \overrightarrow x - \overrightarrow z \).
c) Sai.
Vì hình lập phương có cạnh bằng \(a\) nên \(A'B = A'C' = C'B = a\sqrt 2 \), do đó tam giác \(A'BC'\) đều, nên \(\angle BA'C' = {60^\bigcirc } \Rightarrow \left( {\overrightarrow {BA'} ,\,\overrightarrow {A'C'} } \right) = {180^\bigcirc } - {60^\bigcirc } = {120^\bigcirc }\).
d) Đúng.
Dễ thấy \(ABCD.A'B'C'D'\) nên \(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AM \Rightarrow \)tam giác \(AA'M\) vuông tại \(A\).
Có \(\left| {\overrightarrow {A'M} } \right| = A'M = \sqrt {A{{A'}^2} + A{M^2}} = \sqrt {A{{A'}^2} + A{B^2} + B{M^2}} \)\( = \sqrt {{a^2} + {a^2} + \frac{{{a^2}}}{4}} = \frac{{3a}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

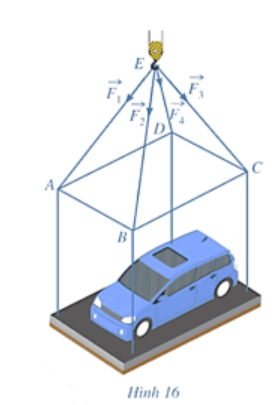
![Cho hình hộp \[ABCD.EFGH\]. Kết quả quả phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/3-1759236661.png)