Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\), mặt phẳng \(\left( {ABCD} \right)\)song song với mặt phẳng nằm ngang. Khung sắt đó được đặt vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA;\,EB;\,EC;\,ED\) bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\)một góc \(\alpha \). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết các lực căng \(\overrightarrow {{F_1}} ;\,\overrightarrow {{F_2}} ;\,\overrightarrow {{F_3}} ;\,\overrightarrow {{F_4}} \) đều có cường độ là \(4800\,N\), trọng lượng của cả khung sắt chứa xe ô tô là \(7200\sqrt 6 \,N\). Tính \(\sin \alpha \) (làm tròn kết quả đến hàng phần trăm).
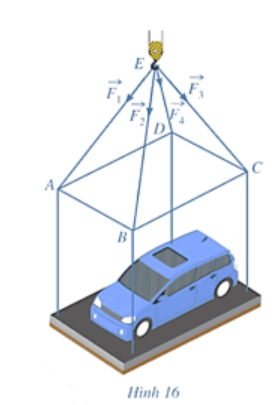
Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt dạng hình hộp chữ nhật với đáy trên là hình chữ nhật \(ABCD\), mặt phẳng \(\left( {ABCD} \right)\)song song với mặt phẳng nằm ngang. Khung sắt đó được đặt vào móc \(E\) của chiếc cần cẩu sao cho các đoạn dây cáp \(EA;\,EB;\,EC;\,ED\) bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\)một góc \(\alpha \). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Biết các lực căng \(\overrightarrow {{F_1}} ;\,\overrightarrow {{F_2}} ;\,\overrightarrow {{F_3}} ;\,\overrightarrow {{F_4}} \) đều có cường độ là \(4800\,N\), trọng lượng của cả khung sắt chứa xe ô tô là \(7200\sqrt 6 \,N\). Tính \(\sin \alpha \) (làm tròn kết quả đến hàng phần trăm).

Câu hỏi trong đề: Đề kiểm tra Vectơ trong không gian (có lời giải) !!
Quảng cáo
Trả lời:

Gọi \({A_1};\,{B_1};\,{C_1};\,{D_1}\) là các điểm thỏa mãn : \(\overrightarrow {E{A_1}} = \overrightarrow {{F_1}} ;\,\,\overrightarrow {E{B_1}} = \overrightarrow {{F_2}} ;\,\,\overrightarrow {E{C_1}} = \overrightarrow {{F_3}} ;\,\,\overrightarrow {E{D_1}} = \overrightarrow {{F_4}} \).
Vì \(EA;\,EB;\,EC;\,ED\) bằng nhau và cùng tạo với mặt phẳng \(\left( {ABCD} \right)\)một góc \(\alpha \) nên \(E{A_1};\,E{B_1};\,E{C_1};\,E{D_1}\) cũng bằng nhau và cùng tạo với mặt phẳng \(\left( {{A_1}{B_1}{C_1}{D_1}} \right)\)một góc \(\alpha \).
Mặt khác \(ABCD\) là hình chữ nhật nên \({A_1}{B_1}{C_1}{D_1}\) cũng là hình chữ nhật có tâm O.
Từ các điều kiện trên ta suy ra \(EO \bot \left( {{A_1}{B_1}{C_1}{D_1}} \right)\). Khi đó \(\alpha = \left( {E{A_1};\,\left( {{A_1}{B_1}{C_1}{D_1}} \right)} \right) = \widehat {E{A_1}O}\).
Ta có: \[\left| {\overrightarrow {{F_1}} } \right| = \,\left| {\overrightarrow {{F_2}} } \right| = \,\left| {\overrightarrow {{F_3}} } \right| = \left| {\,\overrightarrow {{F_4}} } \right| = 4800N\] nên \(E{A_1} = E{B_1} = E{C_1} = E{D_1} = 4800\)
Xét tam giác \(E{A_1}O\) vuông tại O nên \(EO = E{A_1}.\sin \alpha = 4800.\sin \alpha \).
Ta có: \[\overrightarrow {{F_1}} + \,\overrightarrow {{F_2}} + \,\overrightarrow {{F_3}} + \,\overrightarrow {{F_4}} = \overrightarrow {E{A_1}} + \overrightarrow {E{B_1}} + \overrightarrow {E{C_1}} + \overrightarrow {E{D_1}} = 4\overrightarrow {EO} \].
Mặt khác : \[\overrightarrow {{F_1}} + \,\overrightarrow {{F_2}} + \,\overrightarrow {{F_3}} + \,\overrightarrow {{F_4}} = \overrightarrow P \] với \[\overrightarrow P \] là trọng lực tác động lên khung chứa xe ô tô.
Suy ra: \[\overrightarrow P = 4\overrightarrow {EO} \].
Trọng lượng của cả khung sắt chứa xe ô tô là \[|\overrightarrow P | = 4EO = 19200.\sin \alpha \,\,\,\,\,\,\,\,\left( N \right)\].
Theo bài ra ta có: \[19200.\sin \alpha = 7200\sqrt 6 \, \Leftrightarrow \sin \alpha = \frac{{3\sqrt 6 }}{8} \approx 0,92\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)Đ b) S c) S d Đ
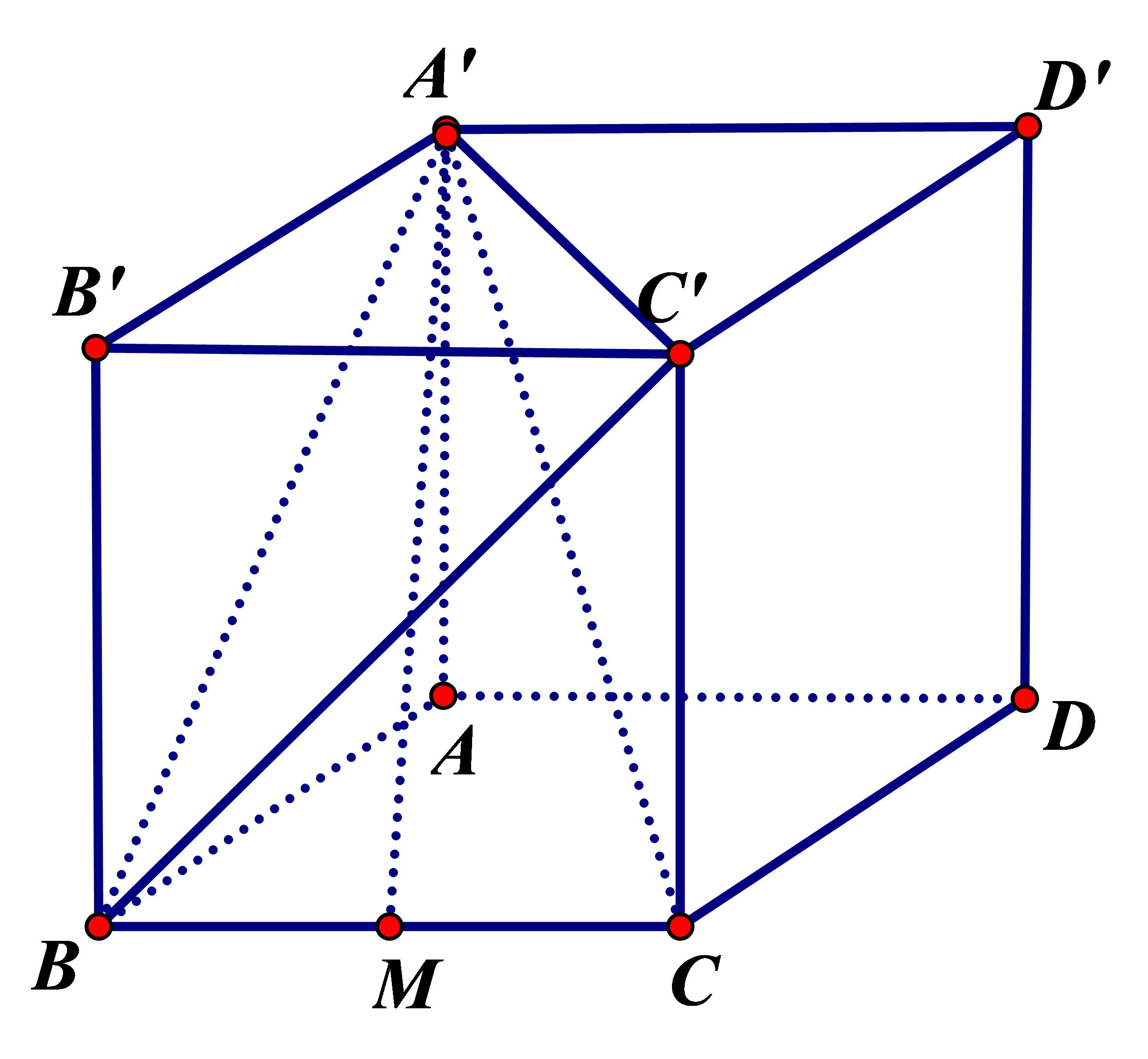
Theo quy tắc hình hộp ta có \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow x + \overrightarrow y + \overrightarrow z \).
b) Sai.
Theo quy tắc 3 điểm ta có \(\overrightarrow {A'B} = \overrightarrow {AB} - \overrightarrow {AA'} = \overrightarrow x - \overrightarrow z \).
c) Sai.
Vì hình lập phương có cạnh bằng \(a\) nên \(A'B = A'C' = C'B = a\sqrt 2 \), do đó tam giác \(A'BC'\) đều, nên \(\angle BA'C' = {60^\bigcirc } \Rightarrow \left( {\overrightarrow {BA'} ,\,\overrightarrow {A'C'} } \right) = {180^\bigcirc } - {60^\bigcirc } = {120^\bigcirc }\).
d) Đúng.
Dễ thấy \(ABCD.A'B'C'D'\) nên \(AA' \bot \left( {ABCD} \right) \Rightarrow AA' \bot AM \Rightarrow \)tam giác \(AA'M\) vuông tại \(A\).
Có \(\left| {\overrightarrow {A'M} } \right| = A'M = \sqrt {A{{A'}^2} + A{M^2}} = \sqrt {A{{A'}^2} + A{B^2} + B{M^2}} \)\( = \sqrt {{a^2} + {a^2} + \frac{{{a^2}}}{4}} = \frac{{3a}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Cho hình hộp \[ABCD.EFGH\]. Kết quả quả phép toán \[\overrightarrow {AB} - \overrightarrow {EH} \] là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/3-1759236661.png)