Bắn một hạt neutron có động năng $K_n$ vào hạt nhân $_3^6$Li đang đứng yên và gây ra phản ứng:
\[
{}^{1}_{0}n + {}^{6}_{3}\text{Li} \;\;\rightarrow\;\; {}^{3}_{1}\text{H} + {}^{4}_{2}\text{He}.
\]
Sau phản ứng, hạt nhân $_2^4$He và hạt nhân $_1^3$H bay ra theo các hướng hợp với hướng tới của hạt neutron các góc lần lượt là $\varphi$ và $120^\circ - \varphi$ như hình vẽ.
Lấy khối lượng các hạt nhân bằng số khối tính theo đơn vị amu. Bỏ qua bức xạ gamma. Biết phản ứng này thu năng lượng 1,87 MeV. Giá trị lớn nhất của $K_n$ gần nhất với giá trị nào sau đây?
Bắn một hạt neutron có động năng $K_n$ vào hạt nhân $_3^6$Li đang đứng yên và gây ra phản ứng:
\[
{}^{1}_{0}n + {}^{6}_{3}\text{Li} \;\;\rightarrow\;\; {}^{3}_{1}\text{H} + {}^{4}_{2}\text{He}.
\]
{}^{1}_{0}n + {}^{6}_{3}\text{Li} \;\;\rightarrow\;\; {}^{3}_{1}\text{H} + {}^{4}_{2}\text{He}.
\]
Sau phản ứng, hạt nhân $_2^4$He và hạt nhân $_1^3$H bay ra theo các hướng hợp với hướng tới của hạt neutron các góc lần lượt là $\varphi$ và $120^\circ - \varphi$ như hình vẽ.
Lấy khối lượng các hạt nhân bằng số khối tính theo đơn vị amu. Bỏ qua bức xạ gamma. Biết phản ứng này thu năng lượng 1,87 MeV. Giá trị lớn nhất của $K_n$ gần nhất với giá trị nào sau đây?
A. 3,8 MeV.
B. 4,6 MeV.
C. 8,3 MeV.
D. 6,4 MeV.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Áp dụng định luật bảo toàn động lượng, ta có:
\[
\vec{p}_n = \vec{p}_{He} + \vec{p}_H \qquad (p_{Li} = 0).
\]
\vec{p}_n = \vec{p}_{He} + \vec{p}_H \qquad (p_{Li} = 0).
\]
Ta có hình vẽ sau:
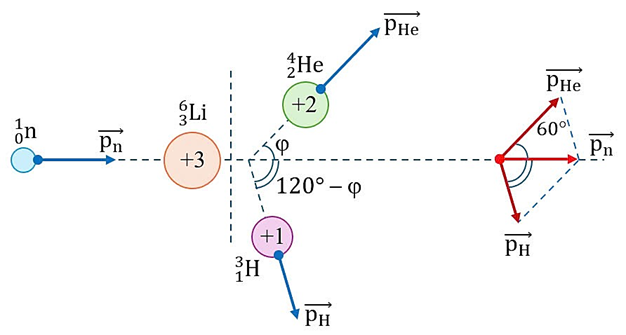
Áp dụng định lí sin, ta có:
\[
\frac{p_{He}}{\sin \varphi}
= \frac{p_H}{\sin(120^\circ - \varphi)}
= \frac{p_n}{\sin 60^\circ}.
\]
Mà: \(p^2 = 2mK\).
Suy ra:
\[
\frac{p_{He}^2}{\sin^2 \varphi}
= \frac{p_H^2}{\sin^2 (120^\circ - \varphi)}
= \frac{p_n^2}{\sin^2 60^\circ}.
\]
\[
\Leftrightarrow
\frac{K_{He}}{\sin^2 \varphi / 2,25}
= \frac{K_H}{\sin^2 (120^\circ - \varphi)/3}
= K_n \quad (1).
\]
Áp dụng định luật bảo toàn năng lượng toàn phần, ta có:
\[
m_n c^2 + K_n + m_{Li} c^2 + K_{Li}
= m_{He} c^2 + K_{He} + m_H c^2 + K_H.
\]
\[
\Leftrightarrow K_n - K_{He} - K_H + (m_n + m_{Li} - m_{He} - m_H)c^2 = 0
\]
\[
\Leftrightarrow K_n - K_{He} - K_H + \Delta E = 0 \quad (2).
\]
Từ (1) và (2), suy ra:
\[
K_n - \frac{\sin^2 (120^\circ - \varphi)}{3}K_n
- \frac{\sin^2 \varphi}{2,25}K_n - 1,87 = 0
\]
\[
\Rightarrow K_n = \frac{1,87}{1 - \dfrac{\sin^2 (120^\circ - \varphi)}{3} - \dfrac{\sin^2 \varphi}{2,25}}.
\]
Sử dụng tính năng \texttt{Table} trên máy tính cầm tay, ta xác định được:
\[
K_{n(\max)} \approx 4,552\ \text{MeV} \quad \text{khi } \varphi \approx 67^\circ.
\]
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Sau khi đổ thêm vào ống thủy tinh một lượng thủy ngân có chiều cao $h$, ta có trạng thái của khối khí trong nhánh kín:
Trạng thái 1:
\[
p_1 = p_0\ \text{(cmHg)}, \qquad
V_1 = \ell_0 S\ \text{(cm}^3), \qquad
T_1.
\]
Trạng thái 2:
\[
p_2 = p_0 + \Delta p
= p_0 + (h - 2\Delta \ell)\ \text{(cmHg)}, \qquad
V_2 = \ell S\ \text{(cm}^3), \qquad
T_2 = T_1,
\]
với \(\Delta \ell = \ell_0 - \ell\).
Áp dụng định luật Bôyle, ta có:
\[
p_1V_1=p_2V_2 \;\Leftrightarrow\; p_0\cdot \ell_0\cdot S = \big[p_0+(h-2\,\Delta\ell)\big]\cdot \ell \cdot S.
\]
Thay số:
\[
76\cdot 30 = \big[76 + \big(h-2\cdot(30-25)\big)\big]\cdot 25
\;\Rightarrow\; h = 25{,}2\ \text{cm}.
\]
Lời giải
|
|
Nội dung |
Đúng |
Sai |
|
a |
Trong quá trình pit tông bắt đầu di chuyển đến khi chất lỏng bắt đầu tràn ra ngoài, áp suất của lượng khí hydrogen không đổi. Sau đó, áp suất của lượng khí hydrogen giảm dần cho đến khi toàn bộ lượng chất lỏng bị tràn ra ngoài. |
Đ |
|
|
b |
Thể tích ban đầu của lượng khí hydrogen là 0,36 lít. |
Đ |
|
|
c |
Công mà lượng khí hydrogen đã thực hiện cho đến khi toàn bộ chất lỏng bị tràn ra ngoài có độ lớn bằng 19,5 J. |
|
S |
|
d |
Từ khi bắt đầu cung cấp nhiệt đến khi toàn bộ chất lỏng bị tràn ra ngoài thì độ biến thiên nội năng của lượng khí hydrogen là 138,5 J. |
|
S |
a) ĐÚNG
Trong quá trình pittông bắt đầu di chuyển đến khi chất lỏng bắt đầu tràn ra ngoài, lượng khí hydrogen được cung cấp nhiệt chậm để pittông di chuyển từ từ, nên áp suất của lượng khí hydrogen không đổi. Sau đó, chất lỏng bắt đầu tràn ra ngoài làm cho áp suất tác dụng lên lượng khí giảm dần.
b) ĐÚNG
Xét quá trình từ khi bắt đầu cung cấp nhiệt đến khi toàn bộ chất lỏng bị tràn ra ngoài:
+ Các trạng thái của lượng khí hydrogen:
+ Quá trình biến đổi trạng thái của lượng khí hydrogen được biểu diễn trên hệ trục tọa độ $(p, V)$ như sau:
\[
\Delta U = \tfrac{5}{2}nR(T_3 - T_1) = A + Q
\]
\[
\Rightarrow \tfrac{5}{2}(p_3V_3 - p_1V_1) = -\Big[ \tfrac{10}{9}p_0\Big(\tfrac{3}{4}V - \tfrac{1}{2}V\Big) + \tfrac{1}{2}\Big(\tfrac{10}{9}p_0 + p_0\Big)\Big(V - \tfrac{3}{4}V\Big)\Big] + 119
\]
\[
\Rightarrow \tfrac{5}{2}(p_0V - \tfrac{10}{9}p_0 \cdot \tfrac{1}{2}V) = -\tfrac{13}{24}p_0V + 119
\]
\[
\Rightarrow \tfrac{10}{9}p_0V = \tfrac{13}{24}p_0V + 119
\]
\[
\Rightarrow \tfrac{119}{72}p_0V = 119
\]
\[
\Rightarrow V = 0,00072\ \text{m}^3 = 0,72\ \ell
\]
Vậy thể tích ban đầu của lượng khí hydrogen là $\tfrac{1}{2}V = 0,36\ \ell$.
c) SAI
Công mà lượng khí hydrogen đã thực hiện cho đến khi toàn bộ chất lỏng bị tràn ra ngoài có độ lớn bằng:
\[
A = \tfrac{13}{24}p_0V = \tfrac{13}{24} \cdot 10^5 \cdot 0,00072 \approx 39\ \text{J}.
\]
d) SAI
Từ khi bắt đầu cung cấp nhiệt đến khi toàn bộ chất lỏng bị tràn ra ngoài thì độ biến thiên nội năng của lượng khí hydrogen là:
\[
\Delta U = A + Q = -39 + 119 = 80\ \text{J}.
\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 4,4 phút.
B. 4,2 phút.
C. 6,5 phút.
D. 4,0 phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. Quá trình ngưng tụ.
B. Quá trình ngưng kết.
C. Quá trình đông đặc.
D. Quá trình nóng chảy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo