Bảng tần số ghép nhóm dưới đây thể hiện kết quả điều tra về tuổi thọ trung bình của nam giới và nữ giới ở 50 quốc gia.

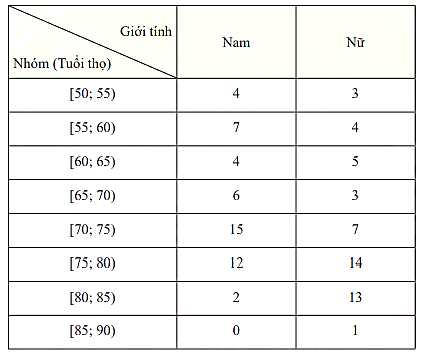
Gọi \(A,B\)lần lượt là khoảng tứ phân vị của nhóm tuổi thọ trung bình của nam và nữ. Tính \(A - B\)( làm tròn đến hàng phần mười).

Một công ty cung cấp nước sạch thống kê lượng nước các hộ gia đình trong một khu vực tiêu thụ trong một tháng ở bảng sau:

a) Có 42 hộ gia đình tiêu thụ lượng nước từ \[9\;{{\rm{m}}^3}\] đến dưới \[12\;{{\rm{m}}^3}.\]

b) Mốt của mẫu số liệu ghép nhóm trên là \(8,0625.\)

c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên xấp xĩ \[5,68.\]

d) Công ty muốn gửi một thông báo khuyến nghị tiết kiệm nước đến 25% các hộ gia đình có lượng nước tiêu thụ cao nhất thì công ty nên gửi thông báo tiết kiệm nước đến các hộ gia đình có lượng nước tiêu thụ từ \(8,95\;{{\rm{m}}^3}\) nước trở lên.

Khảo sát điểm trung bình môn Toán của một số học sinh lớp 12 được cho ở bảng sau:

a) Có 80 học sinh tham gia khảo sát.

b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 4.

c) Có nhiều hơn 50% số học sinh đạt ít nhất 8 điểm.

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là 1,04.

Phần 2. Trắc nghiệm lựa chọn đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Dựa vào bảng tần số mẫu số liệu ghép nhóm sau, hãy xét tính đúng sai của các mệnh đề bên dưới:

a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là \[50.\]

b) Nhóm chứa mốt là nhóm \([50;60).\)

c) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên là: \({Q_1} = 48.\)

d) Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là \[14,5.\]

Khảo sát thời gian (tính bằng giây) chạy cự ly 100 m của 39 học sinh nam, giáo viên thu được mẫu số liệu ghép nhóm sau

a) Thành tích từ 23 giây đến dưới 25 giây có 15 học sinh.

b) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là 13.

c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm là \[4,15.\]

d) Số học sinh đạt thành tích chạy (làm tròn đến hàng phần trăm) xấp xỉ 23,7 giây là nhiêu nhất