Điều tra về chiều cao của học sinh khối lớp 10, ta có kết quả sau:
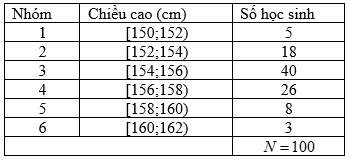
Giá trị đại diện của nhóm thứ tư là
Giá trị đại diện của nhóm thứ tư là
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giá trị đại diện của nhóm thứ tư là: \(\frac{{156 + 158}}{2} = 157\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Cỡ mẫu: \(n = 13 + 35 + 47 + 25 = 120\). Số công nhân có mức thưởng tết từ 15 đến dưới 20 triệu đồng là nhiều nhất nên nhóm chứa mốt là nhóm \[\left[ {15;{\rm{ }}20} \right).\]
Ta có, \({a_j} = 15;{m_j} = 47;{m_{j - 1}} = 35;{m_{j + 1}} = 25;h = 5\). Do đó, mốt của mẫu số liệu là
Ý nghĩa. Số công nhân nhận được mức thưởng tết khoảng 16,76 triệu đồng là cao nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
a) Đúng |
b) Đúng |
c) Sai |
d) Sai |
Cỡ mẫu của mẫu số liệu là \(n = 40\).
Gọi \({x_1},{x_2},{x_3}, \ldots ,{x_{40}}\) là mẫu số liệu được xếp theo thứ tự không giảm.
Trung vị của mẫu số liệu: \(\frac{{{x_{20}} + {x_{21}}}}{2} \in [50;60)\).
Ta có: \({n_m} = 16;{C_2} = 2 + 10 = 12;{u_m} = 50;{u_{n + 1}} = 60\).
Tứ phân vị thứ hai của mẫu số liệu ghép nhóm cũng là trung vị của mẫu số liệu đó là:
\({Q_2} = {M_e} = 50 + \frac{{\frac{{40}}{2} - 12}}{{16}}(60 - 50) = 55\)
Xét nửa mẫu số liệu bên trái \({x_1},{x_2},{x_3}, \ldots ,{x_{20}}\) có trung vị \(\frac{{{x_{10}} + {x_{11}}}}{2} \in [40;50)\).
Ta có: \({n_i} = 10;{C_1} = 2;{u_i} = 40;{u_{i + 1}} = 50\).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_1} = 40 + \frac{{\frac{{40}}{4} - 2}}{{10}}(50 - 40) = 48\)
Xét nửa mẫu số liệu bên phải \({x_{21}},{x_{22}},{x_{23}}, \ldots ,{x_{40}}\) có trung vị \(\frac{{{x_{30}} + {x_{31}}}}{2} \in [60;70)\).
Ta có: \({n_j} = 8;{C_3} = 2 + 10 + 16 = 28;{u_j} = 60;{u_{j + 1}} = 70\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_3} = 60 + \frac{{\frac{{3.40}}{4} - 28}}{8}(70 - 60) = 62,5\)
Vậy tứ phân vị của mẫu số liệu ghép nhóm trên là:
\({Q_1} = 48,{Q_2} = 55,{Q_3} = 62,5.{\rm{ }}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[7,73\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập