Trong không gian Oxyz, phương trình nào trong các phương trình sau là phương trình của một mặt cầu?
Quảng cáo
Trả lời:
Chọn C
Phương trình: \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) \(\left( {{a^2} + {b^2} + {c^2} - d > 0} \right)\) là phương trình mặt cầu có tâm \(I\left( {a\,;\,b\,;\,c} \right)\), bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Ở đáp án A và B không đúng dạng phương trình mặt cầu vì hệ số của \({x^2},{y^2},{z^2}\) không bằng nhau nên phương trình ở đáp án A, B không là phương trình mặt cầu.
Trong đáp án D ta có: \(\left\{ \begin{array}{l}a = 2\\b = - 1\\c = - 1\\d = 8\end{array} \right. \Rightarrow {a^2} + {b^2} + {c^2} - d = - 2 < 0\) nên phương trình ở đáp án D không là phương trình mặt cầu.
Trong đáp án C ta có: \(\left\{ \begin{array}{l}a = 2\\b = - 1\\c = - 1\\d = 2\end{array} \right. \Rightarrow {a^2} + {b^2} + {c^2} - d = 4 > 0\) nên phương trình ở đáp án C là phương trình mặt cầu.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương trình mặt cầu \(\left( S \right):\,{x^2} + {y^2} + {z^2} = 36\).
Ta có \(MA + MB = \sqrt {{{\left( {x - 26} \right)}^2} + {y^2} + {z^2}} + \sqrt {{x^2} + {{\left( {y - 26} \right)}^2} + {z^2}} \).
Áp dụng bất đẳng thức Minkowski ta có:
\(MA + MB = \sqrt {{{\left( {x - 26} \right)}^2} + {y^2} + {z^2}} + \sqrt {{x^2} + {{\left( {y - 26} \right)}^2} + {z^2}} \)\( \ge \sqrt {{{\left( {x + y - 52} \right)}^2} + {{\left( {x + y} \right)}^2} + 4{z^2}} \)
\( \ge \sqrt {{{\left( {x + y - 52} \right)}^2} + {{\left( {x + y} \right)}^2}} \).
Điều kiện để \(MA + MB = \sqrt {{{\left( {x + y - 52} \right)}^2} + {{\left( {x + y} \right)}^2}} \) là khi \(z = 0\), khi đó \(\,{x^2} + {y^2} = 36\)
Mặt khác, vì \(M\left( {x;y;z} \right)\) thuộc mặt cầu tâm \(O\), bán kính bằng 6 nên \( - 6 \le x;y;z \le 6\) dó đó \(x + y > - 12\).
Áp dụng bất đẳng thức Bunhiacopxki, ta có \(x + y \le \sqrt {\left( {{1^2} + {1^2}} \right)\left( {{x^2} + {y^2}} \right)} = \sqrt {2.36} = 6\sqrt 2 \).
Đặt \(t = x + y \Rightarrow - 12 < t \le 6\sqrt 2 \), khi đó \(f\left( t \right) = MA + MB = \sqrt {{{\left( {t - 52} \right)}^2} + {t^2}} = \sqrt {2{t^2} - 104t + {{52}^2}} \).
\(f'\left( t \right) = \frac{{2t - 52}}{{\sqrt {2{t^2} - 104t + {{52}^2}} }}\).
Dễ thấy hàm số \[f'\left( t \right) \le 0\,\]khi \( - 12 < t \le 6\sqrt 2 \). Do đó \(f\left( t \right)\) đạt giá trị nhỏ nhất trên \( - 12 < t \le 6\sqrt 2 \) khi \(t = 6\sqrt 2 \) và bằng \(f\left( {6\sqrt 2 } \right) = \sqrt {2{t^2} - 104t + {{52}^2}} = \sqrt {2776 - 624\sqrt 2 } \approx 44\).
Đáp án: 44.
Lời giải
Gọi \(A,B\) là giao điểm của mp \(\left( Q \right)\) với trục \(Ox\) và \(Oy\), \(H\) là hình chiếu vuông góc của \(O\) lên \(AB\).
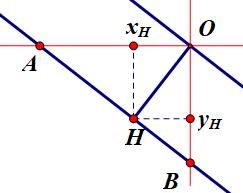
Vì khoảng cách giữa hai mặt phẳng bằng \(30\)m nên \(OH = 30\).
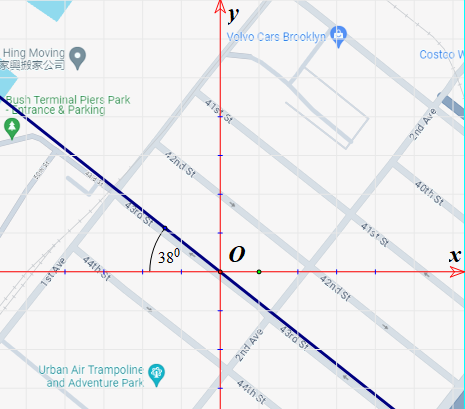
Theo giả thiết ta có góc \(\widehat {OAH} = 38^\circ \) nên khi đó \(OA = \frac{{OH}}{{\sin 38^\circ }} = \frac{{30}}{{\sin 38^\circ }}\).
\({x_H} = - OH.\cos 52^\circ = - 30.\cos 52^\circ \), \({y_H} = - OH\cos 38^\circ = - 30\cos 38^\circ \).
Tọa độ điểm \(A\left( { - \frac{{30}}{{\sin 38^\circ }};\,0\,;\,0} \right)\), \(H\left( { - 30\cos 52^\circ ;\, - 30\cos 38^\circ ;0} \right)\) và chọn một vectơ pháp tuyến là \(\overrightarrow n = \left( {1;\,\frac{{\cos 38^\circ }}{{\cos 52^\circ }}\,;\,0} \right)\).
Mặt phẳng \(\left( Q \right)\) đi qua \(A\) vuông góc \(OH\) nhận \(\overrightarrow n \) làm véc tơ pháp tuyến có phương trình:
\(\left( {x + \frac{{30}}{{\sin 38^\circ }}} \right) + \frac{{\cos 38^\circ }}{{\cos 52^\circ }}y = 0 \Leftrightarrow x + \frac{{\cos 38^\circ }}{{\cos 52^\circ }}y + \frac{{30}}{{\sin 38^\circ }} = 0\).
Vậy \(m + n = 68\).
Đáp án: 68.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.