Hệ Thống Định Vị Vệ Tinh Toàn Cầu Beidou (Bắc Đẩu) hiện tại có 35 vệ tinh, mỗi vệ tinh cách Trái Đất khoảng 35000 km, ta coi Trái Đất là khối cầu có bán kính \(R = 6,4\)(nghìn km). Với hệ tọa độ \(Oxyz\) đã chọn, \(O\) là tâm Trái Đất và đơn vị trên mỗi trục là nghìn km, hai vệ tinh có tọa độ \(A\left( {30;0;0} \right),B\left( {0;30;0} \right)\). Xét điểm \(M\left( {x;y;z} \right)\) thuộc bề mặt Trái Đất. Đặt \(T\) là tổng khoảng cách từ \(M\) đến hai vệ tinh \(A\) và \(B\). Tìm giá trị nhỏ nhất của \(T\) theo đơn vị nghìn km (làm tròn kết quả đến hàng phần chục).
Hệ Thống Định Vị Vệ Tinh Toàn Cầu Beidou (Bắc Đẩu) hiện tại có 35 vệ tinh, mỗi vệ tinh cách Trái Đất khoảng 35000 km, ta coi Trái Đất là khối cầu có bán kính \(R = 6,4\)(nghìn km). Với hệ tọa độ \(Oxyz\) đã chọn, \(O\) là tâm Trái Đất và đơn vị trên mỗi trục là nghìn km, hai vệ tinh có tọa độ \(A\left( {30;0;0} \right),B\left( {0;30;0} \right)\). Xét điểm \(M\left( {x;y;z} \right)\) thuộc bề mặt Trái Đất. Đặt \(T\) là tổng khoảng cách từ \(M\) đến hai vệ tinh \(A\) và \(B\). Tìm giá trị nhỏ nhất của \(T\) theo đơn vị nghìn km (làm tròn kết quả đến hàng phần chục).
Câu hỏi trong đề: Đề kiểm tra Toán 12 Chân trời sáng tạo Chương 5 có đáp án !!
Quảng cáo
Trả lời:
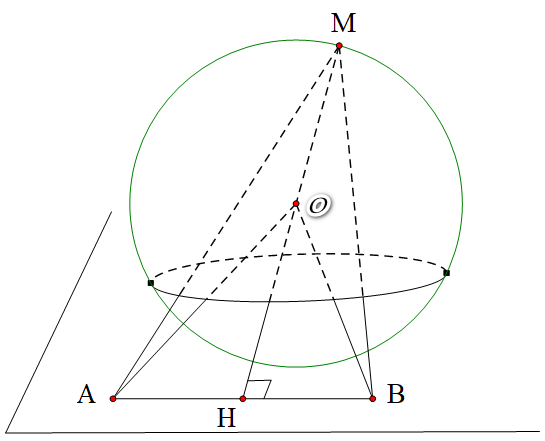
Mặt cầu \(\left( S \right)\) có tâm \(O\left( {0;0;0} \right)\) và bán kính \(R = 6,4\) có phương trình \({x^2} + {y^2} + {z^2} = 40,96\).
Ta có: \(OA = 30;OB = 30;AB = 30\sqrt 2 \). Suy ra \(\Delta OAB\) cân tại \(O\).
Gọi \(H\) là trung điểm của \(AB\), khi đó \(H\left( {15;15;0} \right)\), ta có \(OH \bot AB\).
Đường thẳng \(OH\) đi qua \(O\left( {0;0;0} \right)\) và có VTCP \(\overrightarrow {OH} \left( {15;15;0} \right) = 15\left( {1;1;0} \right)\) là: \(\left\{ \begin{array}{l}x = t\\y = t\\z = 0\end{array} \right.\).
Để \(M \in \left( {OAB} \right)\) thỏa mãn \(MA + MB\) nhỏ nhất thì \(M,A,B\) phải đồng phẳng và \(MA = MB\).
Vì \(MH\) nhỏ nhất nên \(M\) là giao điểm của \(OH\) và mặt cầu \(\left( S \right)\).
Tọa độ \(M\) thỏa mãn phương trình: \({t^2} + {t^2} + {0^2} = 40,96 \Leftrightarrow 2{t^2} = 40,96 \Leftrightarrow t = \pm \frac{{16\sqrt 2 }}{5}\).
Suy ra \[\left[ \begin{array}{l}{M_1}\left( {\frac{{16\sqrt 2 }}{5};\frac{{16\sqrt 2 }}{5};0} \right) \Rightarrow {M_1}H \approx 14,81\\{M_2}\left( {\frac{{ - 16\sqrt 2 }}{5};\frac{{ - 16\sqrt 2 }}{5};0} \right) \Rightarrow {M_2}H \approx 27,61\end{array} \right..\]
Vậy điểm cần tìm là: \[M\left( {\frac{{16\sqrt 2 }}{5};\frac{{16\sqrt 2 }}{5};0} \right)\] .
\(T = MA + MB = 2MA = 2\sqrt {{{\left( {\frac{{16\sqrt 2 }}{5} - 30} \right)}^2} + {{\left( {\frac{{16\sqrt 2 }}{5} - 0} \right)}^2} + {0^2}} \approx 51,7\).
Đáp án: 51,7.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương trình tham số của đường cáp là: \[d:\left\{ \begin{array}{l}x = - 2\\y = 1 - 2k\\z = 5 + 6k\end{array} \right.\begin{array}{*{20}{c}}{}&{\left( {k \in \mathbb{R}} \right)}\end{array}\]
Do tốc độ chuyển động của cabin là \(4\,{\rm{m/s}}\) nên độ dài \(AM = 4t\) \(\left( m \right)\).
Vì vậy sau \[5\] (s) kể từ lúc xuất phát, cabin đến điểm \[M\] thì \(AM = 4.5 = 20\) \(\left( m \right)\).
Vì \[M \in d \Rightarrow M\left( { - 2;1 - 2k;5 + 6k} \right)\].
\[\overrightarrow {AM} = \left( {0; - 2k;6k} \right)\]. Do 2 vec tơ \[\overrightarrow {AM} ;\vec u\] cùng hướng \(k > 0\).
\(AM = 20 \Leftrightarrow \sqrt {{0^2} + 4{k^2} + 36{k^2}} = 20 \Leftrightarrow 40{k^2} = 400 \Leftrightarrow k = \pm \sqrt {10} \).
Vì \(k > 0 \Rightarrow k = \sqrt {10} \).
Vậy tọa độ \[M\left( { - 2;1 - 2\sqrt {10} ;5 + 6\sqrt {10} } \right)\]. Khi đó \[a + 3b + c = - 2 + 3\left( {1 - 2\sqrt {10} } \right) + 5 + 6\sqrt {10} = 6\].
Đáp án: 6.
Lời giải
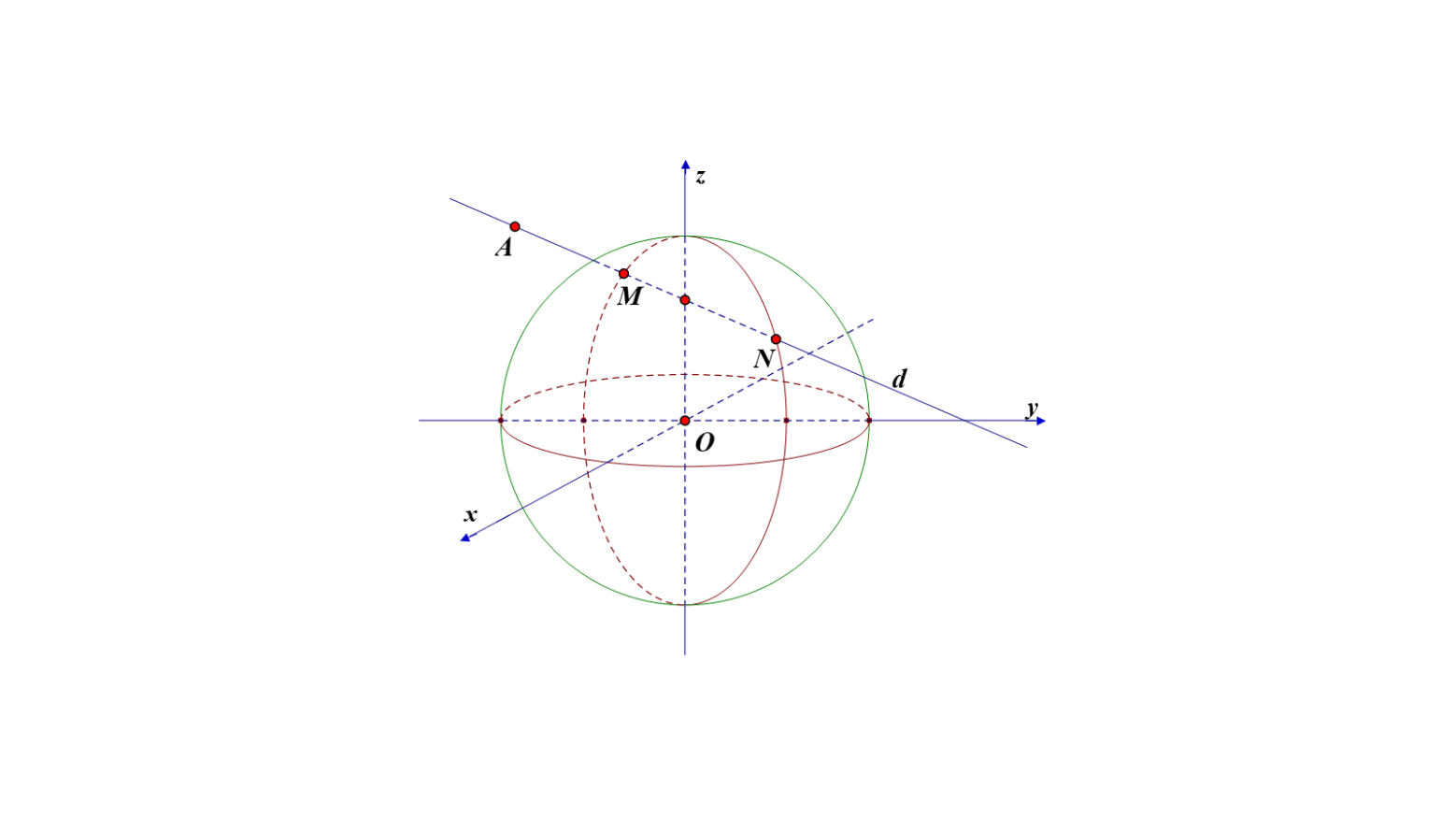
a) Sai. Ta có \(OA = \sqrt {{{\left( { - 65} \right)}^2} + {{\left( { - 25} \right)}^2} + {{30}^2}} \approx 75,8\,{\rm{km}}\).
Khi máy bay ở vị trí \(A\left( { - 65; - 25;30} \right)\) thì cách đài kiểm soát không lưu của sân bay một khoảng \(d \approx 75,8\,{\rm{km}} > 70\,{\rm{km}}\).
Vậy đài kiểm soát không lưu của sân bay không theo dõi được máy bay.
b) Đúng. Từ thông tin của hệ trục và máy bay di chuyển theo hướng Tây Nam với độ cao không đổi, quỹ đạo bay theo đường thẳng. Nên đường thẳng \(d\) có một vectơ chỉ phương \[\overrightarrow u = \left( {1;\,1;\,0} \right)\]. Đường thẳng \(d\) đi qua điểm \(A\left( { - 65; - 25;30} \right)\) nên có phương trình tham số: \(\left\{ \begin{array}{l}x = - 65 + t\\y = - 25 + t\\z = 30\end{array} \right.\).
c) Sai. Thay \(x,\,y,\,z\) theo \(t\) vào phương trình mặt cầu \(\left( S \right)\) ta được phương trình:
\({\left( { - 65 + t} \right)^2} + {\left( { - 25 + t} \right)^2} + {30^2} = 4900 \Leftrightarrow 2{t^2} - 180t + 850 = 0 \Leftrightarrow t = 5\) hoặc \(t = 85\)
Thay \(t = 5\) vào phương trình của đường thẳng \(d\) ta được \(M\left( { - 60; - 20;30} \right)\).
Thay \(t = 85\) vào phương trình của đường thẳng \(d\) ta được \(N\left( {20;60;30} \right)\).
Suy ra đường thẳng \(d\) cắt mặt cầu \(\left( S \right)\) tại hai điểm \(M\left( { - 60; - 20;30} \right)\) và \(N\left( {20;60;30} \right)\).
Hay độ dài đoạn \(MN\) là khoảng cách giữa vị trí đầu tiên và vị trí cuối cùng mà máy bay di chuyển trong phạm vi theo dõi của đài kiểm soát không lưu.
\(MN = \sqrt {{{\left( {60 + 20} \right)}^2} + {{\left( {20 + 60} \right)}^2}} = 80\sqrt 2 \,{\rm{km}}\).
Thời gian máy bay di chuyển trong phạm vi đài kiểm soát không lưu của sân bay theo dõi được là thời gian máy bay di chuyển được quãng đường \(80\sqrt 2 \,{\rm{km}}\).
Thời gian đó bằng \(\frac{{80\sqrt 2 }}{{200}}.60 \approx 33,94\) phút.
d) Đúng. Vùng kiểm không lưu của của đài kiểm soát trên là tập hợp những điểm cách tâm \(O\left( {0;\,\,0;\,\,0} \right)\) không quá \(70\,{\rm{km}}\). Hay tập hợp các điểm ở bên trong và trên bề mặt của mặt cầu \(\left( S \right)\) có phương trình: \({x^2} + {y^2} + {z^2} = {70^2} \Leftrightarrow {x^2} + {y^2} + {z^2} = 4900\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

![Một chiếc bàn gấp gọn đã được thiết lập hệ tọa độ Oxyz. Điểm \[A\] là chân bàn tiếp xúc với mặt đất thuộc đ (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/41-1759843874.png)