Trong 1 lạng thịt bò chứa \(26\;g\) protein, 1 lạng cá chứa \(22\;g\) protein. Trung bình trong một ngày, một người đàn ông cần từ 56 đến \(91\;g\) protein. Theo lời khuyên của bác sĩ, để tốt cho sức khỏe thì không nên ăn thịt nhiều hơn cá. Gọi \(x,y\) lần lượt là số lạng thịt bò, lạng cá mà một người đàn ông ăn trong một ngày. Khi đó:
a) Hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông là \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}26x + 22y \ge 56\\26x + 22y \le 91\\x \le y\\x \ge 0\\y \ge 0\end{array}\end{array}} \right.\)
b) Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông là một ngũ giác
c) \((1;2)\) thuộc miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông
d) Điểm \(B\left( {\frac{{91}}{{48}};\frac{{91}}{{48}}} \right)\) là điểm có hoành độ bé nhất thuộc miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông
Trong 1 lạng thịt bò chứa \(26\;g\) protein, 1 lạng cá chứa \(22\;g\) protein. Trung bình trong một ngày, một người đàn ông cần từ 56 đến \(91\;g\) protein. Theo lời khuyên của bác sĩ, để tốt cho sức khỏe thì không nên ăn thịt nhiều hơn cá. Gọi \(x,y\) lần lượt là số lạng thịt bò, lạng cá mà một người đàn ông ăn trong một ngày. Khi đó:
a) Hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông là \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}26x + 22y \ge 56\\26x + 22y \le 91\\x \le y\\x \ge 0\\y \ge 0\end{array}\end{array}} \right.\)
b) Biểu diễn miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông là một ngũ giác
c) \((1;2)\) thuộc miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông
d) Điểm \(B\left( {\frac{{91}}{{48}};\frac{{91}}{{48}}} \right)\) là điểm có hoành độ bé nhất thuộc miền nghiệm của hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông
Quảng cáo
Trả lời:
|
a) Đúng |
b) Sai |
c) Đúng |
d) Sai |
a) Hệ bất phương trình bậc nhất hai ẩn \(x,y\) để biểu diễn lượng protein cần thiết trong một ngày cho một người đàn ông là: \(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}26x + 22y \ge 56\\26x + 22y \le 91\\x \le y\\x \ge 0\\y \ge 0\end{array}\end{array}} \right.\)
b) Miền nghiệm của hệ trên là miền tứ giác \(ABCD\) với \(A\left( {\frac{7}{6};\frac{7}{6}} \right),B\left( {\frac{{91}}{{48}};\frac{{91}}{{48}}} \right)\), \(C\left( {0;\frac{{91}}{{22}}} \right),D\left( {0;\frac{{28}}{{11}}} \right)\) ở Hình
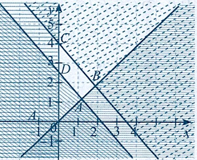
c) Một nghiệm \(\left( {{x_0};{y_0}} \right)\) của hệ bất phương trình với \({x_0},{y_0}\) là \(\left( {{x_0};{y_0}} \right) = (1;2)\).
d) Điểm \(B\left( {\frac{{91}}{{48}};\frac{{91}}{{48}}} \right)\) là điểm có hoành độ lớn nhất
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Miền nghiệm của hệ (I) là miền tứ giác \(ABCD\) với \(A(3;0),B(5;1),C(1;5),D(1;3)\) (Hình).
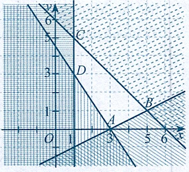
b) \((3;2)\) là một nghiệm của hệ bất phương trình
c) Tính giá trị của \(F = 3x - y\) tại các cặp số \((x;y)\) là toạ độ của các đỉnh tứ giác \(ABCD\) rồi so sánh các giá trị đó, ta được \(F\) đạt giá trị lớn nhất bằng 14 tại \(x = 5,y = 1\)
d) \(F\) đạt giá trị nhỏ nhất bằng \( - 2\) tại \(x = 1,y = 5\).
Lời giải
|
a) Đúng |
b) Sai |
c) Sai |
d) Đúng |
a) Gọi \(x,y\) (đơn vị: triệu đồng) tiền bác Minh đầu tư vào kho Ta có hệ bất phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{x + y \le 240}\\{y \ge 40}\\{x \ge 3y}\end{array}} \right.\)
b) Miền nghiệm của hệ trên là miền tam giác \(ABC\) với \(A(180;60),B(120;40)\), \(C(200;40)\) ở Hình.
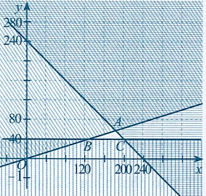
c) Điểm \(C(200;40)\) thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho
d) Điểm \(A(180;60)\) là điểm có tung độ lớn nhất thuộc miền nghiệm của hệ bất phương trình tiền bác Minh đầu tư vào kho
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.