Cho hàm số\[f\left( x \right) = {e^x} + 2x\]. Khẳng định nào dưới đây đúng?
\[\int {f\left( x \right)} = {e^x} + 2x + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} + 2{x^2} + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} - {x^2} + C\].
\[\int {f\left( x \right){\rm{d}}x} = {e^x} + {x^2} + C\].
Câu hỏi trong đề: Đề kiểm tra Toán 12 Cánh diều Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng: D
Ta có \[\int {f\left( x \right){\rm{d}}x} = \int {\left( {{e^x} + 2x} \right)} \,{\rm{d}}x = {e^x} + {x^2} + C\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Thể tích cát ban đầu là: \(\int\limits_0^{20} {v\left( t \right){\rm{d}}t} = \int\limits_0^{20} {0,2t + 13\,{\rm{d}}t} = 300\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
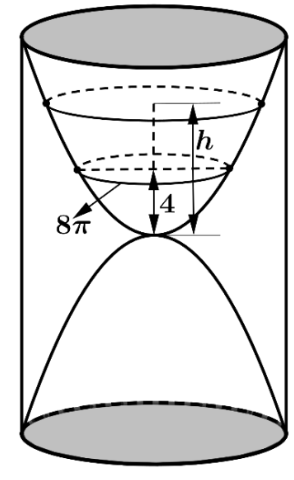
Bán kính đường tròn đáy parabol tròn xoay khi chiều cao cát còn 4cm là: \(\frac{{8\pi }}{{2\pi }} = 4\).
Xét parabol \(\left( P \right):y = a\sqrt x \) đi qua điểm \(A\left( {4;4} \right)\) như hình vẽ
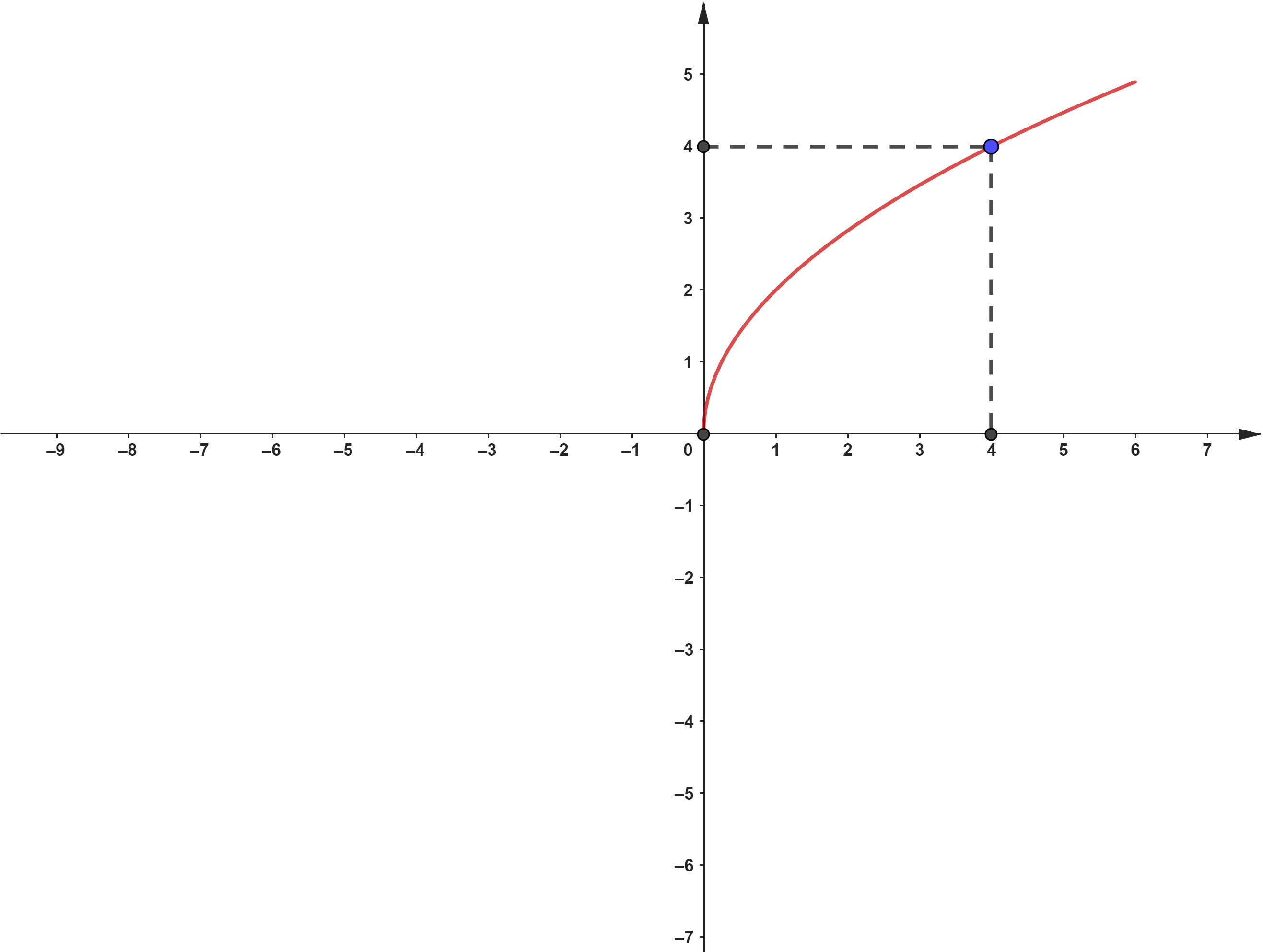
Ta có: \(A\left( {4;4} \right) \in \left( P \right) \Rightarrow 4 = a\sqrt 4 \Rightarrow a = 2\). Suy ra \(\left( P \right):y = 2\sqrt x \).
Khi đó thể tích parabol tròn xoay tạo ra bằng cách xoay hình phẳng giới hạn bởi parabol \(\left( P \right)\), trục \(Ox\) và hai đường thẳng \(x = 0\), \(x = h\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_0^h {{{\left( {2\sqrt x } \right)}^2}{\rm{d}}x} = \frac{{4\pi {x^2}}}{2}\left| {\begin{array}{*{20}{c}}{^h}\\{_0}\end{array}} \right. = 2\pi {h^2}\) (đvtt).
Suy ra: \(2\pi {h^2} = 300\) \( \Rightarrow h = \sqrt {\frac{{150}}{\pi }} \).
Vậy chiều cao khối trụ bên ngoài là: \(2.\left( {\frac{3}{2}.\sqrt {\frac{{150}}{\pi }} } \right) \approx 21\,\,{\rm{cm}}\).
Đáp án: 21.
Lời giải
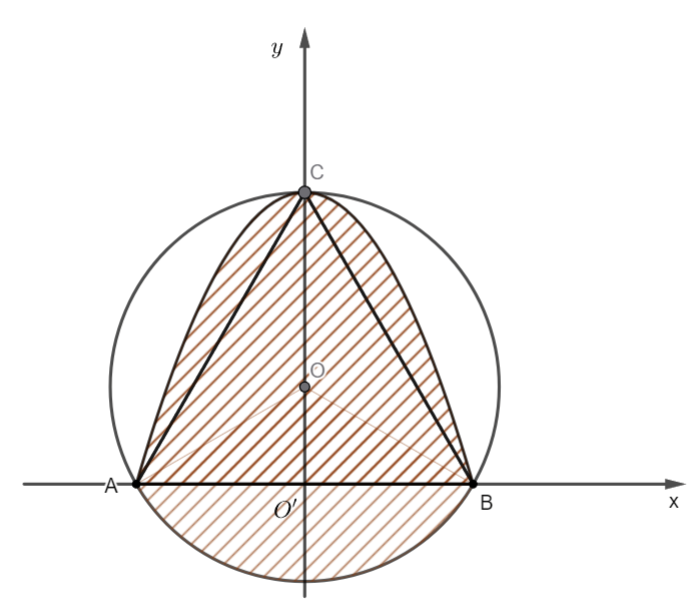
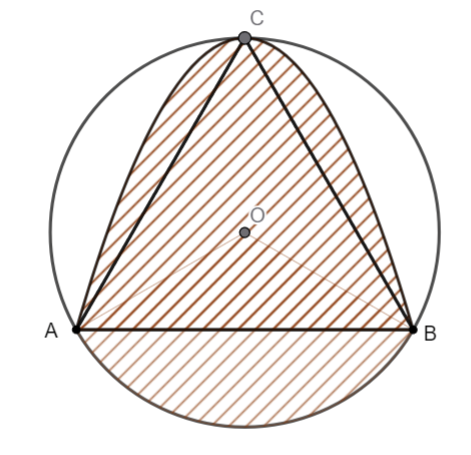
Gắn hệ trục tọa độ \[Oxy\] như hình vẽ.
Khi đó \[A\left( { - \sqrt 3 ;0} \right),B\left( {\sqrt 3 ;0} \right),C\left( {0;3} \right).\]
Parabol đi qua ba điểm \[A\left( { - \sqrt 3 ;0} \right),B\left( {\sqrt 3 ;0} \right),C\left( {0;3} \right)\] nên parabol có phương trình là \[y = - {x^2} + 3.\]
Đường tròn ngoại tiếp tam giác \[ABC\] có tâm \[O\left( {0;1} \right)\] và bán kính \[R = 2\] nên có phương trình là \[{x^2} + {\left( {y - 1} \right)^2} = 4\].
Suy ra \[y = 1 - \sqrt {4 - {x^2}} \] (Phần nằm dưới trục hoành).
Diện tích phần gạch là \[S = \int\limits_{ - \sqrt 3 }^{\sqrt 3 } {\left[ { - {x^2} + 3 - \left( {1 - \sqrt {4 - {x^2}} } \right)} \right]{\rm{d}}x} \].
Do đó diện tích phần không gạch là \[S' = \pi {.2^2} - S \approx 3,18\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right){\rm{.}}\]
Đáp án: 3,18.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\(S = \int\limits_0^7 {( - \sin x + {\rm{cos}}x){\rm{d}}x} \).
\[S = \int\limits_0^7 {\left| {{\rm{sin}}x - {\rm{cos}}x} \right|} {\rm{d}}x\].
\[S = \int\limits_0^7 {({\rm{sin}}x - {\rm{cos}}x){\rm{d}}x} \].
\[S = \int\limits_0^7 {({\rm{sin}}x + {\rm{cos}}x){\rm{d}}x} \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.