Tính diện tích S của hình phẳng (phần gạch sọc) trong hình sau
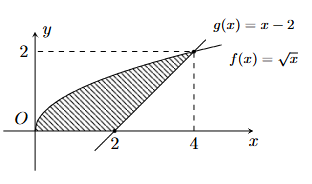
Tính diện tích S của hình phẳng (phần gạch sọc) trong hình sau

A. \(S = \frac{{16}}{3}\).
Quảng cáo
Trả lời:
Chọn A
Diện tích cần tìm là \(S = \int\limits_0^4 {\left| {\sqrt x - \left( {x - 2} \right)} \right|dx} \)\( = \int\limits_0^4 {\left( {\sqrt x - \left( {x - 2} \right)} \right)dx} \)\( = \left. {\left( {\frac{2}{3}{x^{\frac{3}{2}}} - \frac{{{x^2}}}{2} + 2x} \right)} \right|_0^4 = \frac{{16}}{3}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
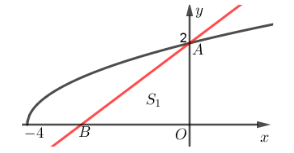
Gọi \(S\) là diện tích hình (H), suy ra \(S = \int\limits_{ - 4}^0 {\sqrt {x + 4} dx} = \frac{{16}}{3}\).
Gọi S1 là diện tích hình (H1) giới hạn bởi đường thẳng d, trục tung và trục hoành.
Do \(d:ax + by - 16 = 0\) đi qua \(A\left( {0;2} \right)\) suy ra \(b = 8\).
Theo giả thiết \({S_1} = \frac{S}{2} = \frac{8}{3}\) mà \({S_1} = \frac{1}{2}OA.OB \Rightarrow OB = \frac{8}{3} \Rightarrow B\left( { - \frac{8}{3};0} \right)\).
Do \(B \in d \Rightarrow a = - 6\).
Vậy \(a + b = 2\).
Trả lời: 2.
Câu 2
Lời giải
Chọn A
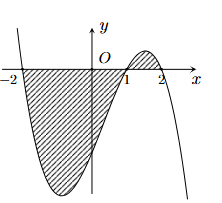
Diện tích cần tìm là \(S = \int\limits_0^\pi {\left| {\cos x} \right|dx} = \int\limits_0^{\frac{\pi }{2}} {\cos xdx} - \int\limits_{\frac{\pi }{2}}^\pi {\cos xdx} \)\( = \left. {\sin x} \right|_0^{\frac{\pi }{2}} - \left. {\sin x} \right|_{\frac{\pi }{2}}^\pi \)\( = 1 + 1 = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.