Cho hàm số \(f\left( x \right)\) xác định trên ℝ\{0} thỏa mãn \(f\left( x \right) = x + 5 - \frac{6}{x}\).
a) f(x) là một nguyên hàm của hàm số \(g\left( x \right) = 1 + \frac{6}{{{x^2}}}\).
b) \(\int {f\left( x \right)dx} = \frac{1}{2}{x^2} + 5x - 6\ln x + C\).
c) Gọi F(x) là một nguyên hàm của hàm số f(x) và thỏa mãn F(1) = 5. Khi đó \(F\left( 2 \right) = 5 + \int\limits_1^2 {f\left( x \right)dx} \).
d) Gọi G(x) là một nguyên hàm của hàm số f(x) thỏa mãn G(1) = 4 và G(2) + G(−1) = 5. Khi đó \(G\left( { - 6} \right) = - 13 - 6\ln 3\).
Cho hàm số \(f\left( x \right)\) xác định trên ℝ\{0} thỏa mãn \(f\left( x \right) = x + 5 - \frac{6}{x}\).
a) f(x) là một nguyên hàm của hàm số \(g\left( x \right) = 1 + \frac{6}{{{x^2}}}\).
b) \(\int {f\left( x \right)dx} = \frac{1}{2}{x^2} + 5x - 6\ln x + C\).
c) Gọi F(x) là một nguyên hàm của hàm số f(x) và thỏa mãn F(1) = 5. Khi đó \(F\left( 2 \right) = 5 + \int\limits_1^2 {f\left( x \right)dx} \).
d) Gọi G(x) là một nguyên hàm của hàm số f(x) thỏa mãn G(1) = 4 và G(2) + G(−1) = 5. Khi đó \(G\left( { - 6} \right) = - 13 - 6\ln 3\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Có \(f'\left( x \right) = 1 + \frac{6}{{{x^2}}} = g\left( x \right)\).
Do đó f(x) là một nguyên hàm của hàm số \(g\left( x \right) = 1 + \frac{6}{{{x^2}}}\).
b) \(\int {f\left( x \right)dx} = \int {\left( {x + 5 - \frac{6}{x}} \right)dx} = \frac{{{x^2}}}{2} + 5x - 6\ln \left| x \right| + C\).
c) Có \(\int\limits_1^2 {f\left( x \right)dx} = \left. {F\left( x \right)} \right|_1^2 = F\left( 2 \right) - F\left( 1 \right)\)\( \Rightarrow F\left( 2 \right) = F\left( 1 \right) + \int\limits_1^2 {f\left( x \right)dx} = 5 + \int\limits_1^2 {f\left( x \right)dx} \).
d) \(G\left( x \right) = \frac{{{x^2}}}{2} + 5x - 6\ln \left| x \right| + C = \left\{ \begin{array}{l}\frac{{{x^2}}}{2} + 5x - 6\ln x + {C_1}\;\;khi\;x \ge 0\\\frac{{{x^2}}}{2} + 5x - 6\ln \left( { - x} \right) + {C_2}\;\;khi\;x < 0\end{array} \right.\).
Ta có \(G\left( 1 \right) = 4 \Rightarrow \frac{1}{2} + 5 + {C_1} = 4 \Rightarrow {C_1} = - \frac{3}{2}\).
Có \(G\left( 2 \right) + G\left( { - 1} \right) = 5\)\( \Leftrightarrow 12 - 6\ln 2 - \frac{3}{2} - \frac{9}{2} + {C_2} = 5 \Rightarrow {C_2} = 6\ln 2 - 1\).
Khi đó \(G\left( { - 6} \right) = \frac{{36}}{2} - 30 - 6\ln 6 + 6\ln 2 - 1 = - 13 - 6\ln 3\).
Đáp án: a) Đúng; b) Sai; c) Đúng; d) Đúng.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
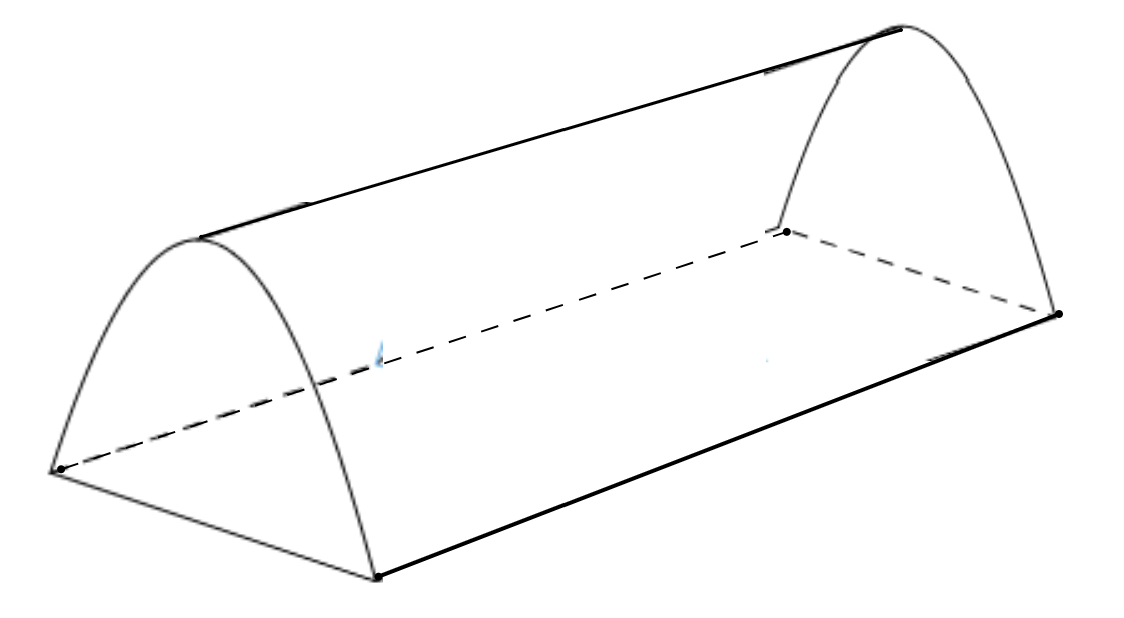
Chọn hệ trục tọa độ như hình vẽ, hình dạng khung trại là parabol có phương trình \(y = f\left( x \right) = a{x^2} + bx + c\), vì đỉnh trại cao 3m và bề ngang rộng 3m nên parabol đi qua điểm \(\left( {0;3} \right)\) và \(\left( {\frac{3}{2};0} \right)\).
Ta có : \[\left\{ \begin{array}{l}b = 0\\3 = c\\0 = a.{\left( {\frac{3}{2}} \right)^2} + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 0\\a = - \frac{4}{3}\\c = 3\end{array} \right.\]
Suy ra parabol có phương trình \(y = f\left( x \right) = - \frac{4}{3}{x^2} + 3\).
Mỗi mặt phẳng vuông góc \[Ox\] tại điểm có hoành độ \[x,\,0 \le x \le h\] cắt khối chóp theo mặt cắt là hình chữ nhật có độ dài các cạnh lần lượt là \[5\] và \[\,\left| {f\left( x \right)} \right|\], có diện tích \(S\left( x \right) = 5.\left| {f\left( x \right)} \right|\) , với \( - \frac{3}{2} \le x \le \frac{3}{2}\).
Vậy thể tích phần không gian trong trại là \(V = \int_{ - \frac{3}{2}}^{\frac{3}{2}} {5.\left| {f\left( x \right)} \right|} dx = 5.\int_{ - \frac{3}{2}}^{\frac{3}{2}} {\left| { - \frac{4}{3}{x^2} + 3} \right|dx = 30\,\,\,{m^3}} \).
Trả lời: 30.
Câu 2
A. 78 cm3.
B. 274 cm3.
C. 87 cm3.
D. 247 cm3.
Lời giải
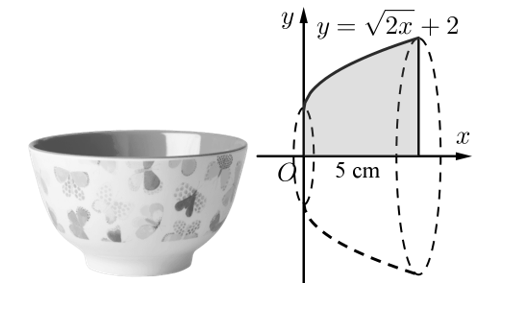
Chọn B
Ta có \(V = \pi \int\limits_0^5 {{{\left( {\sqrt {2x} + 2} \right)}^2}dx} = \pi \int\limits_0^5 {\left( {2x + 4\sqrt {2x} + 4} \right)dx} \)
\( = \left. {\pi \left( {{x^2} + 4\sqrt 2 .\frac{2}{3}{x^{\frac{3}{2}}} + 4x} \right)} \right|_0^5 = \pi \left( {45 + \frac{{40\sqrt {10} }}{3}} \right) \approx 274\) cm3.
Câu 3
A. \(F\left( {\frac{\pi }{2}} \right) = 1\).
B. \(F\left( {\frac{\pi }{2}} \right) = 2\).
C. \(F\left( {\frac{\pi }{2}} \right) = - 1\).
D. \(F\left( {\frac{\pi }{2}} \right) = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(S = \int\limits_c^d {f\left( x \right){\rm{d}}x} - \int\limits_d^0 {f\left( x \right){\rm{d}}x} \).
B. \[S = - \int\limits_c^d {f\left( x \right){\rm{d}}x - \int\limits_d^0 {f\left( x \right){\rm{d}}x} } \].
C. \[S = \int\limits_c^d {f\left( x \right){\rm{d}}x + \int\limits_d^0 {f\left( x \right){\rm{d}}x} } \].
D. \[S = - \int\limits_c^d {f\left( x \right){\rm{d}}x + \int\limits_d^0 {f\left( x \right){\rm{d}}x} } \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo