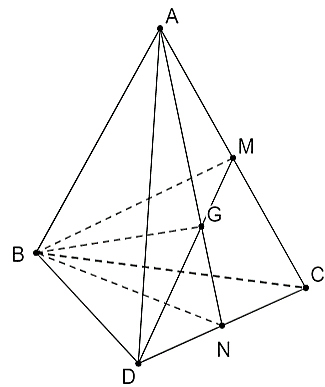
Cho tứ diện \[ABCD\]. Gọi \[M,N\] lần lượt là trung điểm của \[AC,CD\]. Giao tuyến của hai mặt phẳng \[\left( {MBD} \right)\] và \[\left( {ABN} \right)\] là
Câu hỏi trong đề: Bộ 5 đề thi giữa kì 1 Toán 11 cấu trúc mới !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
|
Gọi \[G = AN \cap DM\]. Xét tam giác \[ACD\], có: \[AN,DM\] là các đường trung tuyến của tam giác. Mà \[G = AN \cap DM\] nên \[G\] là trọng tâm tam giác \[ACD\]. Ta có: \[\left\{ \begin{array}{l}BG \subset \left( {MBD} \right)\\BG \subset \left( {ABN} \right)\end{array} \right.\] \[ \Rightarrow \left( {MBD} \right) \cap \left( {ABN} \right) = BG.\] |
 |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
|
a) Đ |
b) S |
c) Đ |
d) Đ |
a) Do theo đề bài, ô thứ nhất nhận 1 hạt tóc, ô thứ hai thì gấp đôi ô thứ nhất, ô thứ 3 thì gấp đôi ô thứ hai, … cứ như vậy ô sau nhận số hạt thóc gấp đôi phần thưởng dành cho ô trước và nhận 64 ô.
Do đó số hạt thóc ở 64 ô lập thành một cấp số nhân với \[{u_1} = 1;{\rm{ }}q = 2.\]
b) Số hạt thóc ở ô thứ 8 sẽ là \[{u_8} = {1.2^7} = {2^7} = 128.\]
c) Tổng số hạt thóc của 64 ô là:
\[S = 1 + 2 + {2^2} + .... + {2^{63}}\]\[ \Rightarrow S = 1.\frac{{1 - {2^{64}}}}{{1 - 2}} = {2^{64}} - 1\] hạt thóc.
Do đó, tổng khối lượng của số hạt thóc trên 64 ô trên bàn cờ là:
\[\left( {{2^{64}} - 1} \right).\frac{{20}}{{100}} \approx 3,{689.10^{18}}\left( g \right)\].
Đổi \[3,{689.10^{18}}{\rm{ }}g = 3,{689.10^{12}}\] (tấn) \[ \approx 369\] (tỉ tấn).
Tương tự, ta có khối lượng thóc ở 32 ô đầu tiên là:
\[\left( {{2^{32}} - 1} \right).\frac{{20}}{{100}} = 858993459\] (g) \[ \approx 859\] tấn.
Vậy cần số chuyến là: \[859:10 = 85,9\] (chuyến).
Vậy cần ít nhất 86 chuyến.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Ta có: \[{u_5} = {u_1}.{q^4} \Leftrightarrow {q^4} = 81 \Leftrightarrow q = \pm 3.\]
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập