(0,5 điểm) Một tấm bìa cứng hình chữ nhật có chiều dài là \({\rm{50 cm}}\)và chiều rộng là \({\rm{30 cm}}\). Bạn Linh cắt ở mỗi góc một tấm bìa hình vuông cạnh \(x{\rm{ }}\left( {{\rm{cm}}} \right)\) và xếp phần còn lại thành một hình hộp không nắp. Tìm \(x\) để diện tích xung quanh của hình hộp chữ nhật sau khi cắt là lớn nhất.

 

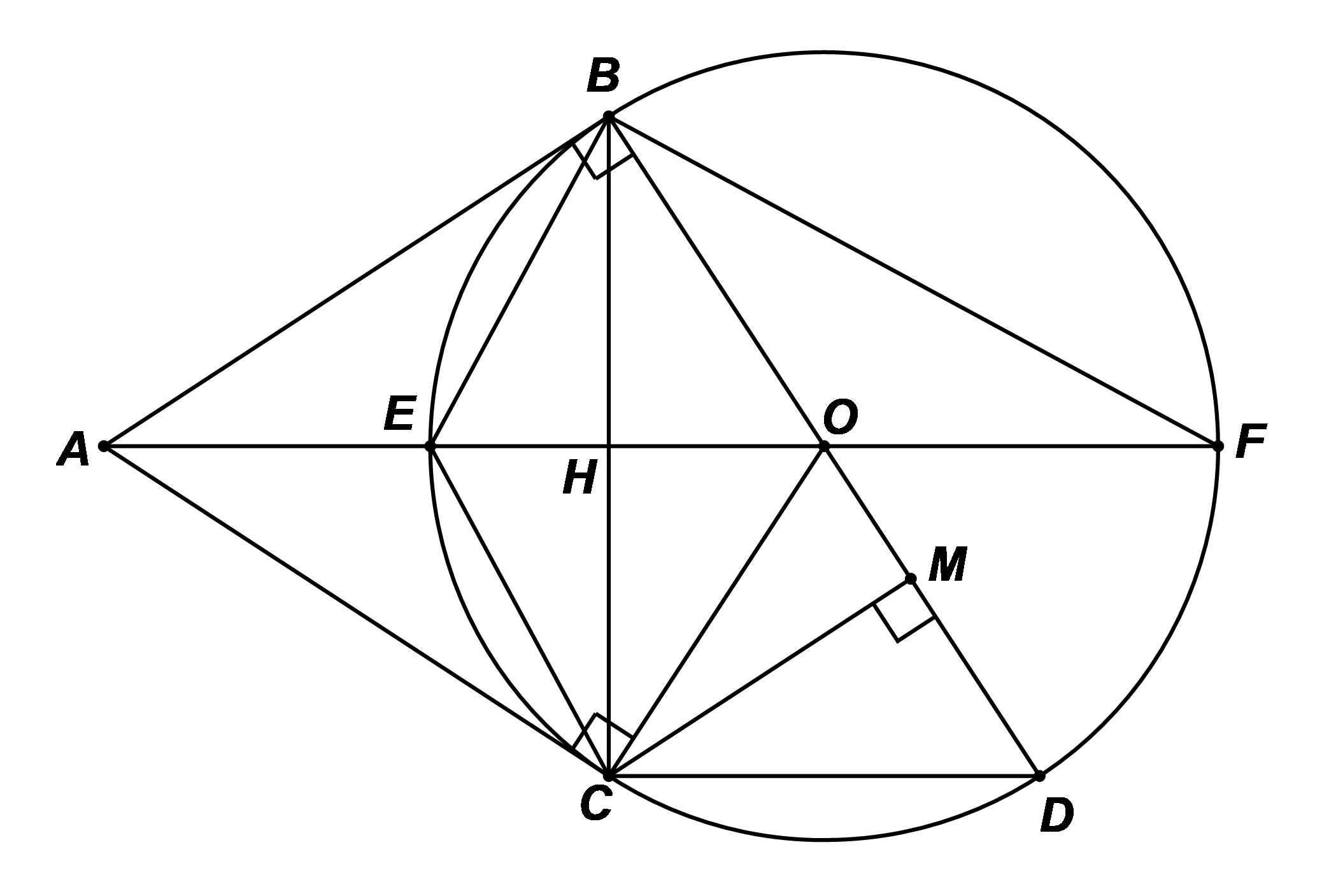
a) Ta có: \(AB,AC\) là hai tiếp tuyến của đường tròn \(\left( O \right)\), suy ra \(OA\) là đường phân giác của \(\widehat {BOC}\) (tính chất) nên \(\widehat {AOC} = \frac{1}{2}\widehat {BOC}.\)

Xét đường tròn \(\left( O \right)\), ta có: \(\widehat {CDB} = \frac{1}{2}\widehat {BOC}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(BC\))

Do đó, \(\widehat {AOC} = \widehat {CDB}\).

Xét \(\Delta CMD\) và \(\Delta ACO\) có:

\(\widehat {CMD} = \widehat {ACO} = 90^\circ \) và \(\widehat {CDM} = \widehat {AOC}\) (do \(\widehat {AOC} = \widehat {CDB}\))

Do đó (g.g).

b) Xét đường tròn \(\left( O \right)\), ta có: \(\widehat {EBF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).

Ta có \(\widehat {ABO} = \widehat {EBF} = 90^\circ \) nên \(\widehat {ABE} + \widehat {EBO} = \widehat {EBO} + \widehat {OBF}\)

Suy ra \(\widehat {ABE} = \widehat {OBF}\).

Lại có: \(\widehat {OBF} = \widehat {OFB}\) (vì \(\Delta BOF\) cân tại \(O\) do \(OB = OF)\) suy ra \(\widehat {ABE} = \widehat {OFB}\) (1)

Mà \(\widehat {ECB} = \widehat {OFB}\) (hai góc nội tiếp cùng chắn cung \(EC\) của đường tròn tâm \(O\)) (2)

Từ (1) và (2) suy ra \(\widehat {ECB} = \widehat {ABE}\). (3)

Mặt khác, \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau) và \(OB = OC = R\)

Suy ra \(OA\) là đường trung trực của \(BC\) mà \(E \in OA\), suy ra \(EB = EC\).

Do đó \(\Delta EBC\) cân tại \(E\) nên \(\widehat {ECB} = \widehat {EBC}\). (4)

Từ (3) và (4) suy ra \(\widehat {EBC} = \widehat {ABE}\) nên \(BE\) là tia phân giác của góc \(B\) trong tam giác \(ABH\).

Vậy \[BE\] là phân giác của \(\widehat {ABC}.\)

c) Theo câu a, (g.g), suy ra \(\widehat {OAC} = \widehat {DCM} = 30^\circ \).

Suy ra \(\widehat {AOC} = 90^\circ - \widehat {OAC} = 90^\circ - 30^\circ = 60^\circ \).

Do đó, \(\widehat {BOC} = 2\widehat {AOC} = 120^\circ \) hay

Xét \(\Delta AHC\) vuông tại \(H\), có: \(\cos \widehat {HAC} = \frac{{AH}}{{AC}}\)

Suy ra \(AC = \frac{{AH}}{{\cos \widehat {HAC}}} = \frac{4}{{\cos 30^\circ }} = \frac{{8\sqrt 3 }}{3}{\rm{ }}\left( {{\rm{cm}}} \right).\)

Xét \(\Delta AOC\) vuông tại \(C\), có: \(OC = AC.\tan \widehat {OAC} = \frac{{8\sqrt 3 }}{3}.\tan 30^\circ = \frac{8}{3}{\rm{ }}\left( {{\rm{cm}}} \right).\)

Diện tích hình quạt giới hạn bởi các bán kính \[OB,OC\] và cung nhỏ \(BC\) là:

\[S = \frac{{\pi .{{\left( {\frac{8}{3}} \right)}^2} \cdot 120}}{{360}} = \frac{{64\pi }}{{27}}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].

Hướng dẫn giải

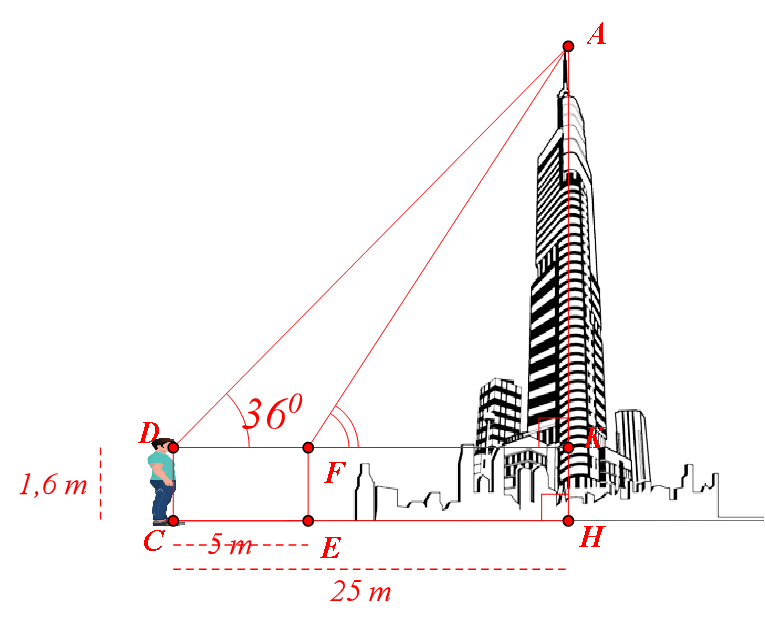
Đáp án đúng là: a) Đúng.  b) Sai.              c) Sai.                  d) Đúng.

• Xét \[\Delta AKD\] vuông tại \[D\], ta có: \[\tan 36^\circ = \tan D = \frac{{AK}}{{KD}}\]O10-2024-GV154......... hay \[AK = AD \cdot \tan 36^\circ \].

Do đó, ý a) là đúng.

• Ta có: \[FK = EH = CH - CE = 25 - 5 = 20{\rm{\;(m)}}{\rm{.}}\]O10-2024-GV154.........

Do đó, ý b) là đúng.

• Từ \[\tan 36^\circ = \tan D = \frac{{AK}}{{KD}},\] ta có \[AK = KD \cdot \tan 36^\circ = 25 \cdot \tan 36^\circ \approx 18,164{\rm{\;(m)}}{\rm{.}}\]

Ta có \[AH = AK + KH \approx 18,164 + 1,6 = 19,764 \approx 20{\rm{\;(m)}}{\rm{.}}\]

Vậy độ dài tòa nhà chính là độ dài đoạn \[AH\] và khoảng 20 m.

Do đó, ý c) là sai.

• Xét \[\Delta AFK\] vuông tại \[K\], ta có: \[\tan F = \frac{{AK}}{{KF}} \approx \frac{{18,164}}{{20}}\]O10-2024-GV154........., do đó \[\widehat {KFA} \approx 42^\circ .\]

Vậy góc nâng từ \[F\] đến nóc tòa nhà khoảng \[42^\circ \].

Vậy ý d) là đúng.