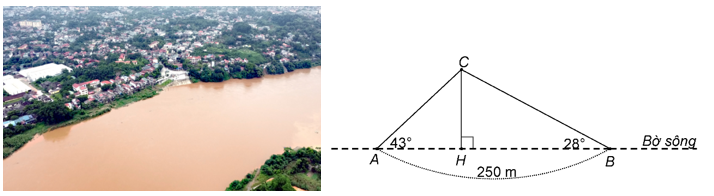
Hai người A và B đứng cùng bờ sông nhìn ra một cồn C nổi giữa sông. Người A nhìn ra cồn với một góc \(43^\circ \) so với bờ sông, người B nhìn ra cồn với một góc \(28^\circ \) so với bờ sông. Hai người đứng cách nhau \(250{\rm{ m}}\) như hình minh họa dưới đây. (Kết quả làm tròn đến hàng phần trăm)
a) \(CH = AH \cdot \tan 43^\circ .\)
b) \(BH = \frac{{CH}}{{\tan 28^\circ }}.\)
c) \(AB = \left( {\tan 43^\circ + \tan 28^\circ } \right)CH\).
d) Cồn cách bờ sông hai người đứng một khoảng lớn hơn \(85{\rm{ m}}{\rm{.}}\)
Hai người A và B đứng cùng bờ sông nhìn ra một cồn C nổi giữa sông. Người A nhìn ra cồn với một góc \(43^\circ \) so với bờ sông, người B nhìn ra cồn với một góc \(28^\circ \) so với bờ sông. Hai người đứng cách nhau \(250{\rm{ m}}\) như hình minh họa dưới đây. (Kết quả làm tròn đến hàng phần trăm)

a) \(CH = AH \cdot \tan 43^\circ .\)
b) \(BH = \frac{{CH}}{{\tan 28^\circ }}.\)
c) \(AB = \left( {\tan 43^\circ + \tan 28^\circ } \right)CH\).
d) Cồn cách bờ sông hai người đứng một khoảng lớn hơn \(85{\rm{ m}}{\rm{.}}\)
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Đúng. c) Sai. d) Sai.
Khoảng cách của cồn và bờ sông hai người đứng chính là độ dài đoạn thẳng \(CH.\)
• Xét tam giác \(AHC\) vuông tại \(H\), ta có: \(\tan \widehat {CAH} = \frac{{CH}}{{AH}}\) nên \(AH = \frac{{CH}}{{\tan \widehat {CAH}}} = \frac{{CH}}{{\tan 43^\circ }}\)
Suy ra \(CH = AH \cdot \tan 43^\circ .\)
Do đó, ý a) là đúng.
• Xét tam giác \(BHC\) vuông tại \(H\), ta có:
\(\tan \widehat {CBH} = \frac{{CH}}{{BH}}\) nên \(BH = \frac{{CH}}{{\tan \widehat {CBH}}} = \frac{{CH}}{{\tan 28^\circ }}\) (2)
Do đó, ý b) là đúng.
• Từ (1) và (2) ta có:
\(AB = AH + BH = \frac{{CH}}{{\tan 43^\circ }} + \frac{{CH}}{{\tan 28^\circ }} = CH\left( {\frac{1}{{\tan 43^\circ }} + \frac{1}{{\tan 28^\circ }}} \right)\)
Do đó, ý c) là sai.
• Do đó, \(CH = \frac{{AB}}{{\frac{1}{{\tan 43^\circ }} + \frac{1}{{\tan 28^\circ }}}} = \frac{{250}}{{\frac{1}{{\tan 43^\circ }} + \frac{1}{{\tan 28^\circ }}}} \approx 84,66{\rm{ (m)}}{\rm{.}}\)
Vậy cồn cách bờ sông hai người đứng khoảng \(84,66{\rm{ m}}\).
Vậy ý d) là sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Gọi số máy móc công ty nên sử dụng là \(x\) máy \(\left( {x > 0,\,x \in \mathbb{N}} \right)\).
Trong một giờ số quả bóng tennis sản xuất được là \(30x\) (quả bóng).
Như vậy, số giờ để sản xuất \(8\,000\) quả bóng tennis là \(\frac{{8\,000}}{{30x}}\) giờ.
Mỗi giờ phải trả \(192\,000\)đồng cho người giám sát và chi phí thiết lập cho mỗi máy là 200 nghìn đồng nên chi phí sản xuất là
\(B = 200\,000x + \frac{{8\,000}}{{30x}} \cdot 192\,000 = 200\,000x + \frac{{51\,200\,000}}{x}\) (đồng)
Với hai số không âm \(a\) và \(b\) ta có \({\left( {\sqrt a - \sqrt b } \right)^2} \ge 0\) suy ra \(a + b \ge 2\sqrt {ab} \).
Áp dụng bất đẳng thức trên với hai số dương \(200\,000x\) và \(\frac{{51\,200\,000}}{x}\), ta được:
\(200\,000x + \,\frac{{51\,200\,000}}{x} \ge 2\sqrt {200\,000x \cdot \frac{{51\,200\,000}}{x}} = 6\,400\,000\)
Dấu “=” xảy ra khi \(200\,000x = \frac{{51\,200\,000}}{x}\) hay \({x^2} = 256\) suy ra \(x = 16\) (do \(x > 0,\,x \in \mathbb{N}\))
Vậy số máy móc công ty nên sử dụng là 16 máy để chi phí sản xuất là thấp nhất.
Lời giải
Hướng dẫn giải
a) Với \(a \ge 0,\,\,a \ne 4,\,\,a \ne 9\), ta có:
\(A = \frac{3}{{\sqrt a + 3}}:\left( {\frac{{\sqrt a - 2}}{{\sqrt a + 3}} + \frac{{\sqrt a - 3}}{{2 - \sqrt a }} - \frac{{9 - a}}{{a + \sqrt a - 6}}} \right)\)
\( = \frac{3}{{\sqrt a + 3}}:\left[ {\frac{{{{\left( {\sqrt a - 2} \right)}^2}}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}} - \frac{{\left( {\sqrt a - 3} \right)\left( {\sqrt a + 3} \right)}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}} - \frac{{9 - a}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}}} \right]\)
\( = \frac{3}{{\sqrt a + 3}}:\left[ {\frac{{a - 4\sqrt a + 4}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}} - \frac{{a - 9}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}} - \frac{{9 - a}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}}} \right]\)
\( = \frac{3}{{\sqrt a + 3}}:\left[ {\frac{{a - 4\sqrt a + 4 - a + 9 - 9 + a}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}}} \right]\)
\( = \frac{3}{{\sqrt a + 3}}:\left[ {\frac{{a - 4\sqrt a + 4}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}}} \right]\)
\( = \frac{3}{{\sqrt a + 3}}:\frac{{{{\left( {\sqrt a - 2} \right)}^2}}}{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}}\)
\( = \frac{3}{{\sqrt a + 3}} \cdot \frac{{\left( {\sqrt a + 3} \right)\left( {\sqrt a - 2} \right)}}{{{{\left( {\sqrt a - 2} \right)}^2}}}\)
\( = \frac{3}{{\sqrt a - 2}}\).
Vậy với \(a \ge 0,{\rm{ }}a \ne 4,{\rm{ }}a \ne 9\) ta được \(P = \frac{3}{{\sqrt a - 2}}\).
b) Ta có: \(A + \left| A \right| = 0\) suy ra \(\left| A \right| = - A\).
Do đó, \(A \le 0\) hay \(\frac{3}{{\sqrt a - 2}} \le 0\) suy ra \(\sqrt a - 2 < 0\) do đó \(\sqrt a < 2\).
Suy ra \(0 \le a < 4\).
Vậy \(0 \le a < 4\) là giá trị cần tìm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
