Trong không gian Oxyz, cho hai đường thẳng 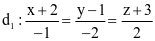 ;
; 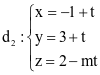 .
.
(a) Khi m = 0, số đo góc giữa hai đường thẳng d1 và d2 bằng 135°.
(b) 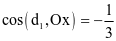 .
.
(c) Đường thẳng △ đi qua gốc tọa độ O và vuông góc với (P): 2x + 2y + z – 4 = 0 tạo với đường thẳng d1 một góc α có 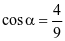 .
.
(d) Khi 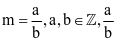 là phân số tối giản, số đo góc giữa hai đường thẳng d1 và d2 bằng 90°. Giá trị biểu thức
là phân số tối giản, số đo góc giữa hai đường thẳng d1 và d2 bằng 90°. Giá trị biểu thức 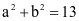 .
.
Quảng cáo
Trả lời:
Đường thẳng d 1 có vectơ chỉ phương là 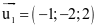
a) Khi m = 0, đường thẳng d 2 có vectơ chỉ phương là 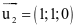 .
.
Khi đó 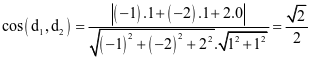 .
.
Suy ra (d 1 , d 2 ) = 45°.
b) Trục Ox có vectơ chỉ phương là 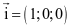 .
.
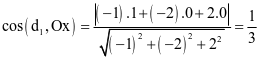 .
.
c) Mặt phẳng (P) có vectơ pháp tuyến 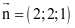 ,
,
Đường thẳng △ đi qua gốc tọa độ O và vuông góc với (P) nên có vectơ chỉ phương là 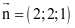 .
.
Khi đó 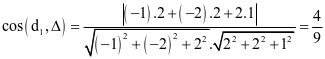 .
.
d) Số đo góc giữa hai đường thẳng d 1 và d 2 bằng 90° khi hai đường thẳng vuông góc.
Khi đó 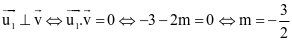 .
.
Suy ra 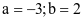 . Vậy
. Vậy 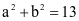 .
.
Đáp án: a) Sai; b) Sai; c) Đúng; d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Để vận động viên bắn trúng hồng tâm thì A ∈ d.
Khi đó 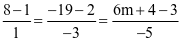
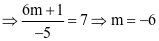 .
.
Trả lời: −6.
Lời giải
Đáp án đúng: C
Đường thẳng d có 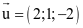 là một vectơ chỉ phương.
là một vectơ chỉ phương.
Vì đường thẳng đi qua A và song song với d nhận 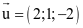 làm một vectơ chỉ phương có phương trình là
làm một vectơ chỉ phương có phương trình là
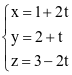 hay
hay 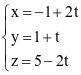 .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
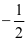 .
.
0.
1.
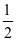 .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
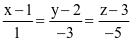 và hồng tâm A(8; −19; 6m + 4). Hỏi m bằng bao nhiêu vận động viên đó bắn trúng hồng tâm?
và hồng tâm A(8; −19; 6m + 4). Hỏi m bằng bao nhiêu vận động viên đó bắn trúng hồng tâm?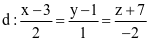 . Đường thẳng đi qua A và song song với d có phương trình là
. Đường thẳng đi qua A và song song với d có phương trình là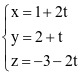 .
.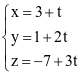 .
.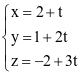 .
.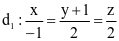 và
và 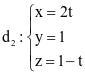 . Gọi
. Gọi 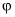 là góc giữa hai đường thẳng d1, d2. Giá trị
là góc giữa hai đường thẳng d1, d2. Giá trị 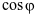 có dạng
có dạng 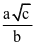 . Tính giá trị biểu thức
. Tính giá trị biểu thức 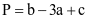 .
.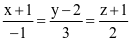 .
.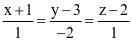 .
.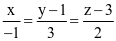 .
.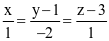 .
.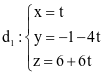 và
và 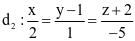 . Phương trình chính tắc của đường thẳng d3 đi qua M(1; −1; 2) và vuông góc với cả d1; d2 có dạng
. Phương trình chính tắc của đường thẳng d3 đi qua M(1; −1; 2) và vuông góc với cả d1; d2 có dạng 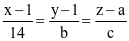 . Tính a + b + c.
. Tính a + b + c.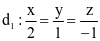 và
và 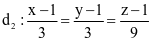 . Khi đó cosα bằng
. Khi đó cosα bằng