Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \sqrt {3{x^2} - {x^3}} \).
a) Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).
b) Hàm số đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2;3} \right)\).
c) Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2;3} \right)\).
d) Đồ thị hàm số có hai cực trị.
Phần II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, chọn đúng hoặc sai.
Cho hàm số \(y = \sqrt {3{x^2} - {x^3}} \).
a) Hàm số đồng biến trên khoảng \(\left( {0;2} \right)\).
b) Hàm số đồng biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2;3} \right)\).
c) Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2;3} \right)\).
d) Đồ thị hàm số có hai cực trị.
Quảng cáo
Trả lời:
Điều kiện: \(3{x^2} - {x^3} \ge 0 \Leftrightarrow x \le 3\).
Có \(y' = \frac{{6x - 3{x^2}}}{{2\sqrt {3{x^2} - {x^3}} }},\forall x \ne 3;x \ne 0\).
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\).
Bảng biến thiên:
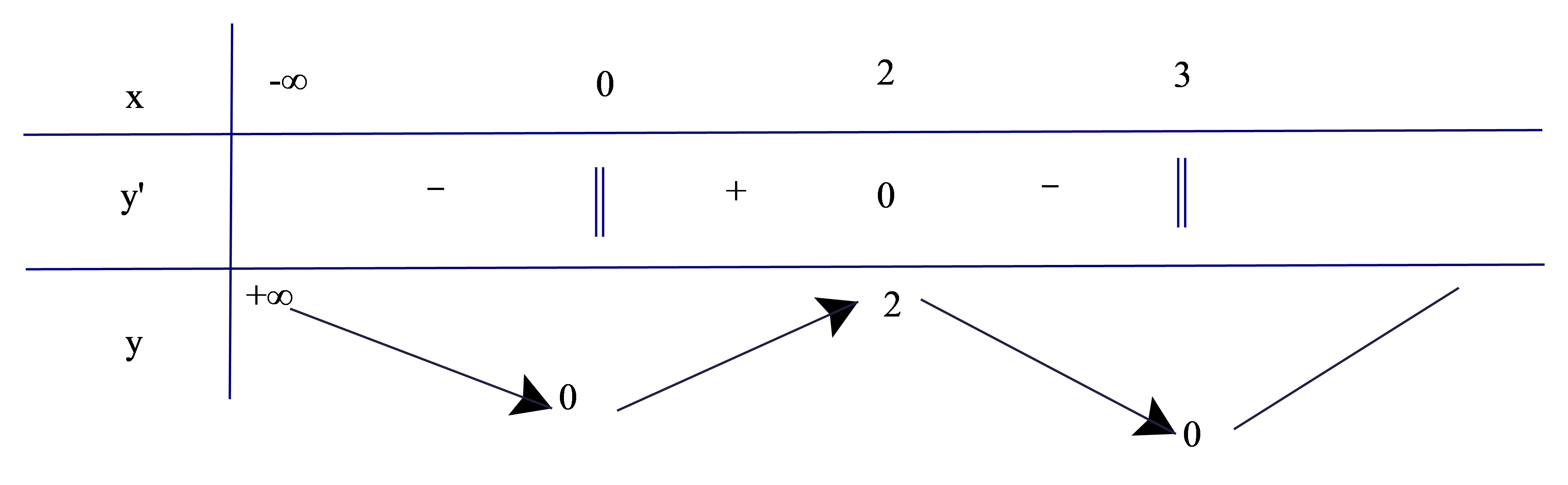
Dựa vào bảng biến thiên ta có:
Hàm số nghịch biến \(\left( { - \infty ;0} \right)\) và \(\left( {2;3} \right)\).
Hàm số đồng biến \(\left( {0;2} \right)\).
Đồ thị hàm số có hai cực trị .
Đáp án: a) Đúng; b) Sai; c) Đúng; d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có \(y = \frac{{{x^2} + 3x + 3}}{{x + 2}}\) suy ra \(y' = \frac{{\left( {2x + 3} \right)\left( {x + 2} \right) - \left( {{x^2} + 3x + 3} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\).
b) \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 3\\x = - 1\end{array} \right.\)\( \Rightarrow y\left( { - 3} \right) = - 3\); \(y\left( { - 1} \right) = 1\).
Suy ra \(A\left( { - 3\,;\, - 3} \right)\) và \(B\left( { - 1\,;\,1} \right)\)
Do \({x_A}.{x_B} = 3 > 0\) nên \(A\) và \(B\) nằm ở cùng một phía của trục tung.
c) Ta có \(\overrightarrow {AB} = \left( {2\,;\,4} \right)\).
Suy ra đường thẳng \(AB\) có phương trình là \( - 2\left( {x + 1} \right) + \left( {y - 1} \right) = 0\)\( \Leftrightarrow y = 2x + 3\).
d) Đường thẳng \(\Delta \) có phương trình là \(x + 2y + 4 = 0\) nên \(\Delta \) có vectơ pháp tuyến \(\overrightarrow {{n_\Delta }} = \left( {1\,;\,2} \right)\).
\(\overrightarrow {AB} = \left( {2\,;\,4} \right)\)
Suy ra \(\overrightarrow {{n_\Delta }} \) và \(\overrightarrow {AB} \) cùng phương với nhau. Do đó \(AB \bot \Delta \).
Ta có \(I\left( { - 2\,;\, - 1} \right)\) là trung điểm của đoạn thẳng \(AB\) và \(I \in \Delta \).
Vậy \(A\) và \(B\) đối xứng nhau qua đường thẳng \(\Delta \).
Đáp án: a) Đúng; b) Sai; c) Sai; d) Đúng.
Lời giải
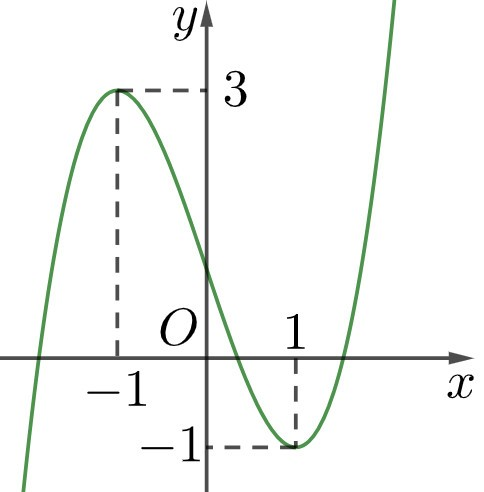
a) Hàm số \(y = f(x)\) đồng biến trên các khoảng \(( - \infty ; - 1)\) và \((1; + \infty ).\)
b) Giá trị cực đại là y = 3, giá trị cực tiểu là y = –1.
Do đó tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho là 3 – 1 = 2.
c) Hàm số \(y = f(x)\)có hai cực trị là \(x = \pm 1.\)
d) Gọi \[d:y = {\rm{ax}} + b\] là đường thẳng qua hai điểm cực trị \[A( - 1;3),B(1; - 1).\]
\[A,B \in d \Rightarrow \left\{ \begin{array}{l} - a + b = 3\\a + b = - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = - 2\\b = 1\end{array} \right. \Rightarrow d:y = - 2x + 1\].
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.
Câu 3
B. \[\left( {0; + \infty } \right).\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
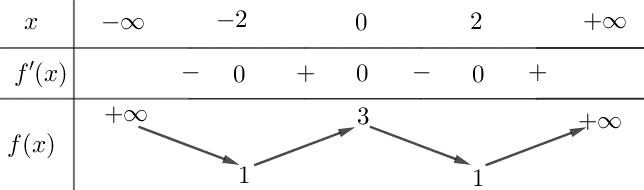
![Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu của đạo hàm như hình vẽ. Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị? A. \[1\]. B. \[2\]. C. \[3\]. D. \[4\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/2-1761387632.png)