Một nhà máy có hai phân xưởng I và II. Phân xưởng I sản xuất 40% số sản phẩm và phân xưởng II sản xuất 60% số sản phẩm. Tỉ lệ sản phẩm bị lỗi của phân xưởng I là 2% và của phân xưởng II là 1%. Kiểm tra ngẫu nhiên 1 sản phẩm của nhà máy và xác suất để sản phẩm đó bị lỗi là
Quảng cáo
Trả lời:
Chọn C
Gọi A là biến cố “Sản phẩm đó thuộc phân xưởng I”; B là biến cố “Sản phẩm đó bị lỗi”.
Ta có \(P\left( A \right) = 0,4;P\left( {\overline A } \right) = 0,6;P\left( {B|A} \right) = 0,02;P\left( {B|\overline A } \right) = 0,01\).
Khi đó \(P\left( B \right) = P\left( A \right).P\left( {B|A} \right) + P\left( {\overline A } \right).P\left( {B|\overline A } \right)\)\( = 0,4.0,02 + 0,6.0,01 = 0,014\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi A là biến cố “Bệnh nhân đó hồi phục sau đột quỵ”;
B là biến cố “Bệnh nhân đó được điều trị trong 6 giờ đầu”.
Theo đề ta có \(P\left( A \right) = 0,35;P\left( B \right) = 0,4;P\left( {AB} \right) = 0,3\).
a) \(P\left( {B|A} \right) = \frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{{0,3}}{{0,35}} \approx 0,86\).
b) \(P\left( {\overline A |B} \right) = \frac{{P\left( {\overline A B} \right)}}{{P\left( B \right)}} = \frac{{P\left( B \right) - P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{0,4 - 0,3}}{{0,4}} = \frac{1}{4}\).
c) \(P\left( {A|\overline B } \right) = \frac{{P\left( {A\overline B } \right)}}{{P\left( {\overline B } \right)}} = \frac{{P\left( A \right) - P\left( {AB} \right)}}{{P\left( {\overline B } \right)}} = \frac{{0,35 - 0,3}}{{0,6}} = \frac{1}{{12}}\).
d) Có \(\frac{{P\left( {A|B} \right)}}{{P\left( {A|\overline B } \right)}} = \frac{{P\left( {AB} \right)}}{{P\left( B \right).P\left( {A|\overline B } \right)}} = \frac{{0,3}}{{0,4.\frac{1}{{12}}}} = 9\).
Đáp án: a) Sai; b) Sai; c) Sai; d) Sai.
Lời giải
Chọn B
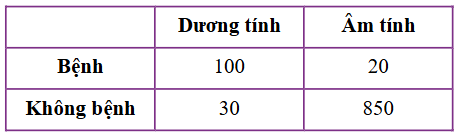
Gọi A là biến cố “Người đó thực sự bị mắc bệnh”; B là biến cố “người đó có kết quả xét nghiệm dương tính”.
Theo đề ta có \(P\left( A \right) = \frac{{120}}{{1000}} = \frac{3}{{25}}\); \(P\left( B \right) = \frac{{130}}{{1000}} = \frac{{13}}{{100}}\); \(P\left( {B|A} \right) = \frac{{100}}{{120}} = \frac{{10}}{{12}}\).
Khi đó \(P\left( {A|B} \right) = \frac{{P\left( A \right).P\left( {B|A} \right)}}{{P\left( B \right)}} = \frac{{\frac{3}{{25}}.\frac{{10}}{{12}}}}{{\frac{{13}}{{100}}}} \approx 77\% \).
Câu 3
A. \(\frac{3}{4}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.