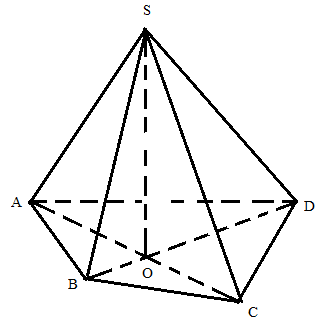
Cho tứ diện \[ABCD\] có \[M,\,\,N\] lần lượt là trung điểm của \[BC\] và \[CD.\] Gọi \[K\] là điểm tuỳ ý thuộc miền trong tam giác \[ABD.\] Giao tuyến của \[\left( {KMN} \right)\] và \[\left( {ABD} \right)\] có tính chất là:
Câu hỏi trong đề: Bộ 19 đề thi Giữa kì 1 Toán 11 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
![Chọn A Ta thấy \[K\] là một điểm chu (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/2-1761530731.png)
Ta thấy \[K\] là một điểm chung của hai mp \[\left( {ABD} \right)\] và \[\left( {KMN} \right)\].
Gọi \[Kx = \left( {ABD} \right) \cap \]\[\left( {IKJ} \right)\,.\]
Ta có: \[IJ\] là đường trung bình của tam giác \[ABC\]\[ \Rightarrow IJ//AB.\]
\[ \Rightarrow \left\{ \begin{array}{l}MN \subset \left( {IJK} \right)\\AB \subset \left( {ABD} \right)\\MN//BD\\\left( {AB{\rm{D}}} \right) \cap \left( {IKJ} \right)\, = Kx\end{array} \right. \Rightarrow Kx//BD\].
Vậy giao tuyến là đường thẳng qua \[K\] và song song với \[BD.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \({u_n}\)là số tiền bạn An nợ ngân hàng sau \(n\) năm
Ta có: \({u_1} = {u_{n - 1}} + {u_{n - 1}}.0,04 = {u_{n - 1}}.1,04\)
Ta có dãy số: \(\left( {{u_n}} \right)\)lập thành một cấp số nhân với số hạng đầu \({u_1} = 40 + 40.0,04 = 41,6\) (triệu đồng) và công bội \(q = 1,04\)
Vậy số tiền bạn An nợ ngân hàng sau 4 năm là:
\({u_4} = {u_1}.{q^3} = 41,6.1,{04^3} = 46,8\)(triệu đồng).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Trong mặt phẳng \[\left( {ABCD} \right)\], gọi \[E = AB \cap CD\].
Trong \[\left( {SAB} \right)\] gọi \[N = SB \cap EM\].
Ta có \[N \in EM \subset \left( {MCD} \right) \Rightarrow N \in \left( {MCD} \right)\] và \[N \in SB\] nên \[N = SB \cap \left( {MCD} \right)\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập