Cho hình lăng trụ \(ABC.A'B'C'\). Gọi \(M\), \(N\) lần lượt là trung điểm của \(BB'\) và \(CC'\). Gọi \(\Delta \) là giao tuyến của hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {A'B'C'} \right)\). Khẳng định nào sau đây đúng?
Câu hỏi trong đề: Bộ 19 đề thi Giữa kì 1 Toán 11 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
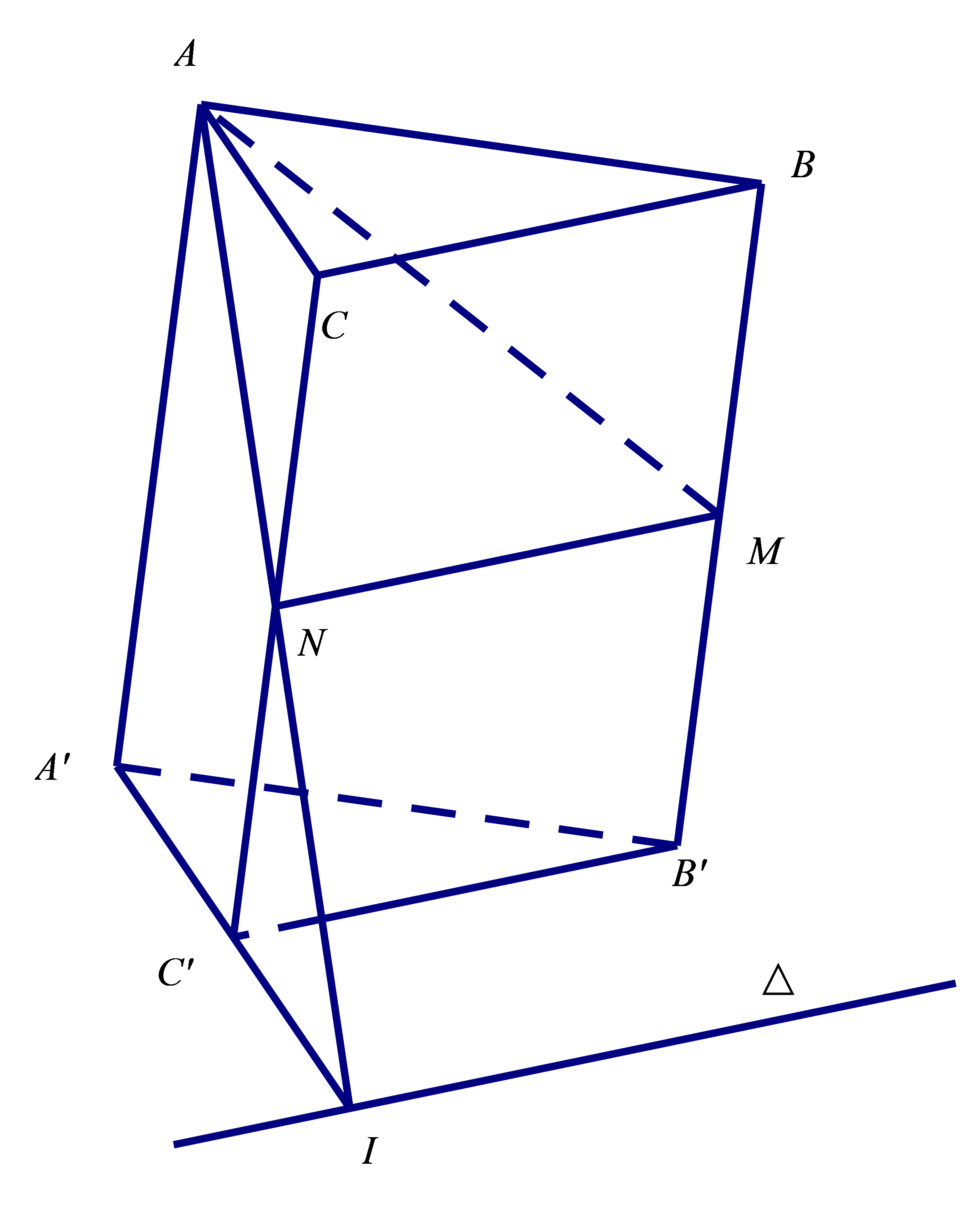
Theo bài ra ta có: \(BC\,{\rm{//}}\,MN{\rm{//}}\,B'C'\).
Trong \(\left( {ACC'A'} \right)\) gọi \(I = AN \cap A'C'\).
Khi đó hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {A'B'C'} \right)\) có điểm chung \(I\) và lần lượt đi qua hai đường thẳng song song \(MN\); \(B'C'\).
Do đó, giao tuyến của hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {A'B'C'} \right)\) là đường thẳng \(\Delta \) qua \(I\) và song song với \(B'C'\)\( \Rightarrow \Delta \,{\rm{//}}\,BC\).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Một bức tường có \[2,72:0,08 = 34\] hàng gạch.
Số gạch ở mỗi hàng tạo thành một cấp số cộng với số hạng đầu \[{u_1} = 1\] và công sai \[d = 1\].
Số viên gạch trên một bức tường: \[{S_{34}} = 34.1 + \frac{{34.33}}{2}.1 = 595\] viên gạch.
Vì 4 mặt đều bằng nhau nên có \[4.595 = 2380\] viên gạch người chủ dự tính đặt mua.
Lời giải
Ta thấy số tấm pin mặt trời mà công ty X lắp đặt hàng tháng lập thành một cấp số nhân \(({u_n})\). Trong đó \[{u_1} = 1200\] tấm và công bội \(q = 1,21\).
Vì công ty cần công suất khoảng \({\rm{2426000W}}p\) để vận hành nên cần phải lắp đặt ít nhất \[5514\] tấm pin mặt trời nghĩa là \[{u_n} = 5514\] tấm.
Mà \[{u_n} = {u_1}.{q^{n - 1}}\] nên \[5514 = 1200.{(1,21)^{n - 1}} \Leftrightarrow n - 1 \approx 8 \Leftrightarrow n \approx 9\].
Vậy công ty cần công suất khoảng \({\rm{2426000W}}p\)để vận hành thì phải lắp pin mặt trời trong ít nhất 9 tháng mới đủ công suất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập