PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (tham khảo hình vẽ). Nghiên cứu trò chơi này, người ta thấy khoảng cách \(h\) (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian \(t(s)\) (với \(t \ge 0\)) vởi hệ thức \(h = |d|\) với \(d = 3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right]\), trong đó ta quy ước \(d > 0\) khi vị trí cân bằng ở phía sau lưng người chơi đu và \(d < 0\) trong trường hợp ngược lại (Nguồn: Đại số và giải tích 11 Nâng cao, NXBGD Việt Nam, 2022). Vào thời điểm \(t\) nào thì khoảng cách \(h\) là \(3\) m; \(0\) m?
PHẦN IV. Câu hỏi tự luận. Thí sinh trình bày lời giải vào giấy làm bài.
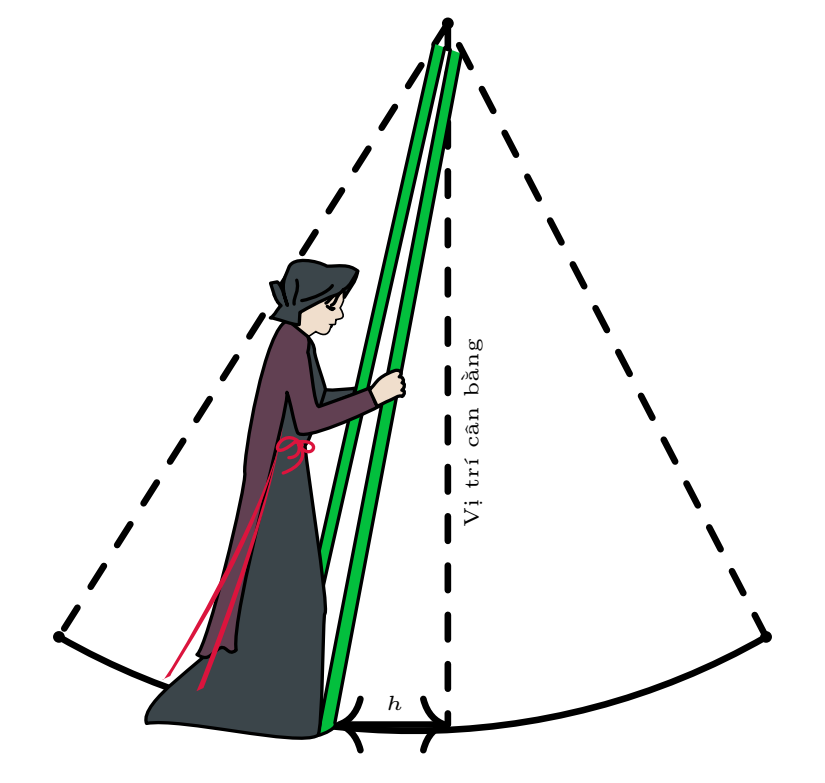
Hội Lim (tỉnh Bắc Ninh) được tổ chức vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (tham khảo hình vẽ). Nghiên cứu trò chơi này, người ta thấy khoảng cách \(h\) (m) từ vị trí người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian \(t(s)\) (với \(t \ge 0\)) vởi hệ thức \(h = |d|\) với \(d = 3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right]\), trong đó ta quy ước \(d > 0\) khi vị trí cân bằng ở phía sau lưng người chơi đu và \(d < 0\) trong trường hợp ngược lại (Nguồn: Đại số và giải tích 11 Nâng cao, NXBGD Việt Nam, 2022). Vào thời điểm \(t\) nào thì khoảng cách \(h\) là \(3\) m; \(0\) m?
Câu hỏi trong đề: Bộ 19 đề thi Giữa kì 1 Toán 11 có đáp án !!
Quảng cáo
Trả lời:
Khoảng cách \(h\) là \(3\) m khi
\(3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right] = - 3 \Leftrightarrow \cos \left[ {\frac{\pi }{3}(2t - 1)} \right] = - 1 \Leftrightarrow \frac{\pi }{3}(2t - 1) = - \pi + k2\pi \Leftrightarrow t = - 1 + 3k,k \in \mathbb{Z}.\)
Vậy vào thời điểm \(t = - 1 + 3k,k \in \mathbb{Z}\) thì khoảng cách \(h\) là \(3\) m.
Khoảng cách \(h\) là \(0\) m khi
\(3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right] = 0 \Leftrightarrow \cos \left[ {\frac{\pi }{3}(2t - 1)} \right] = 0 \Leftrightarrow \frac{\pi }{3}(2t - 1) = \frac{\pi }{2} + k\pi \Leftrightarrow t = \frac{5}{4} + \frac{3}{2}k,k \in \mathbb{Z}.\)
Vậy vào thời điểm \(t = \frac{5}{4} + \frac{3}{2}k,k \in \mathbb{Z}\) thì khoảng cách \(h\) là \(0\) m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số giờ nắng gắt trong ngày thứ \[n\] được tính bởi công thức: \(f\left( n \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {n - 80} \right)} \right] + 12\)
Vậy Tỉnh Quảng Nam chịu nhiều giờ nắng gắt nhất nghĩa là \(f\left( n \right)\) đạt giá trị lớn nhất
Ta có: \( - 1 \le \sin \left[ {\frac{\pi }{{182}}\left( {n - 80} \right)} \right] \le 1,\,\forall n\) \( \Rightarrow f\left( n \right) \le 15\)
Suy ra \(\max f\left( n \right) = 15 \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {n - 80} \right)} \right] = 1\)
\( \Leftrightarrow \frac{\pi }{{182}}\left( {n - 80} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow n = 171 + k.364,\forall k \in \mathbb{Z}\)
Mà \(0 < n \le 365\) nên \(n = 171\).
Đán án: 171
Lời giải
Hình vuông \({A_1}\) có diện tích \({S_1} = 1\)
Hình vuông \({A_2}\) là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông \({A_1}\) do đó hình vuông
\({A_2}\) có diện tích \({S_2} = \frac{1}{2}{S_1} = \frac{1}{2}\)
Tương tự, hình vuông \({A_3}\) có diện tích \({S_3} = \frac{1}{2}{S_2} = \frac{1}{2}.\frac{1}{2} = \frac{1}{{{2^2}}}\)
Cứ tiếp tục như thế ta tính được diện tích hình vuông \({A_{2024}}\) là \({S_{2024}} = \frac{1}{{{2^{2023}}}}\)
Câu 3
A. Tứ giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.