Cho tứ diện \(SABC\). Trên đoạn \(SC\) lấy điểm \(M\) sao cho \(3SM = 2MC\). Gọi \(N\), \(K\) lần lượt là trung điểm của các cạnh \(BC\), \(SA\). Gọi \(I\) là giao điểm của đường thẳng \(AB\) và mặt phẳng \(\left( {KMN} \right)\). Biết \(AB = 2\sqrt 3 \). Độ dài cạnh \(IA\) bằng bao nhiêu? (Làm tròn kết quả đến hai chữ số thập phân)
Câu hỏi trong đề: Bộ 19 đề thi Giữa kì 1 Toán 11 có đáp án !!
Quảng cáo
Trả lời:
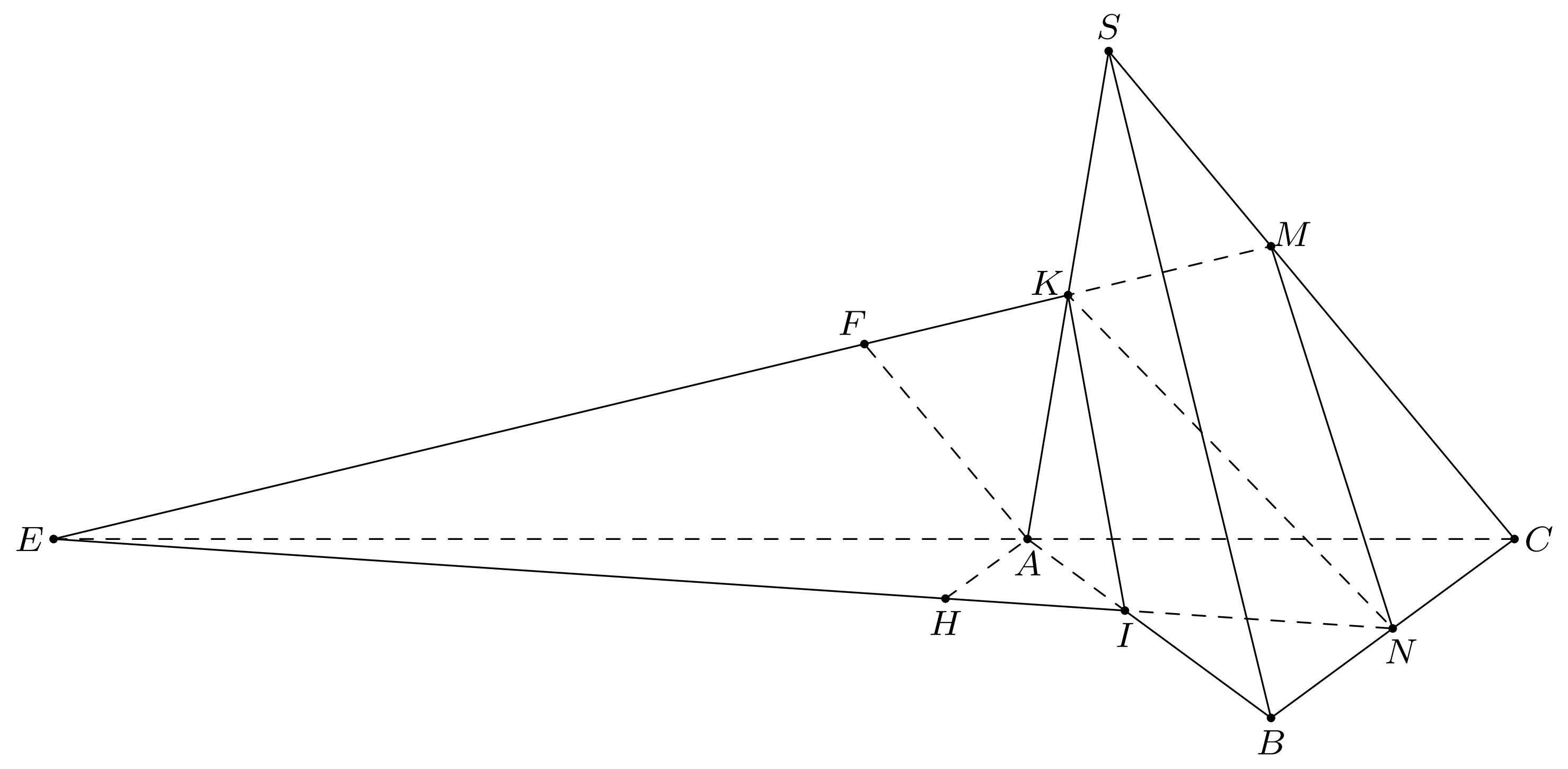
Trong \(\left( {SAC} \right)\), gọi \(E = AC \cap KM\), dựng \(AF\parallel SC\), \(F \in EM\).
.
Ta có \(\frac{{SM}}{{CM}} = \frac{2}{3} \Rightarrow \frac{{AF}}{{CM}} = \frac{2}{3}\).
Trong có \(AF\parallel CM \Rightarrow \frac{{EA}}{{EC}} = \frac{{AF}}{{CM}} = \frac{2}{3}\).
Trong \(\left( {ABC} \right)\) dựng \(AH\parallel BC\), \(H \in EN \Rightarrow \frac{{AH}}{{NC}} = \frac{{EA}}{{EC}} = \frac{2}{3} \Rightarrow \frac{{AH}}{{NB}} = \frac{2}{3}\).
Ngoài ra có .
Suy ra \(IA = \frac{2}{5}AB = \frac{2}{5} \cdot 2\sqrt 3 = \frac{{4\sqrt 3 }}{5} \approx 1,39\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
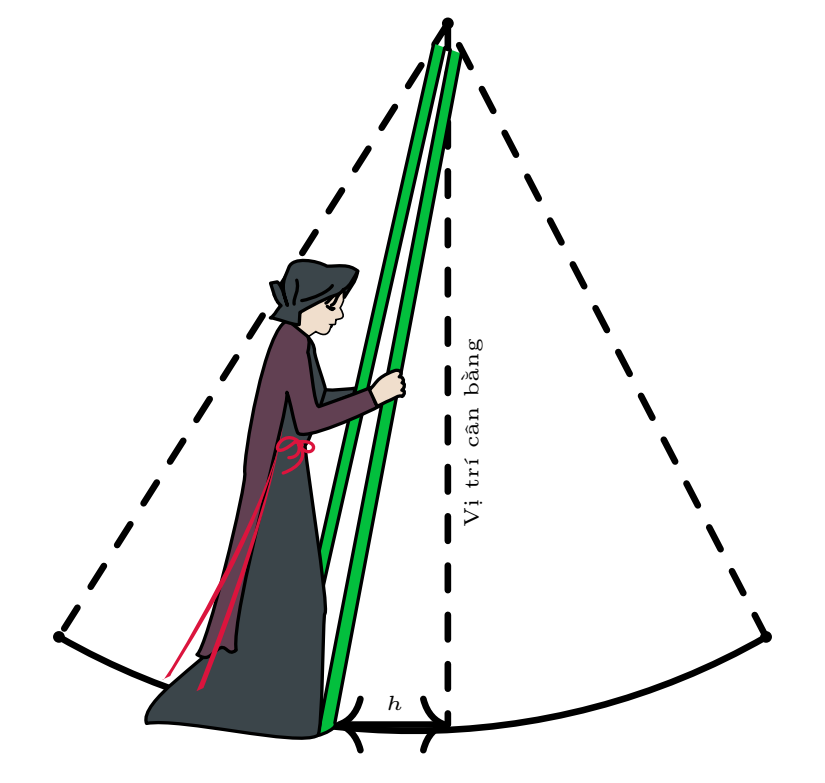
Khoảng cách \(h\) là \(3\) m khi
\(3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right] = - 3 \Leftrightarrow \cos \left[ {\frac{\pi }{3}(2t - 1)} \right] = - 1 \Leftrightarrow \frac{\pi }{3}(2t - 1) = - \pi + k2\pi \Leftrightarrow t = - 1 + 3k,k \in \mathbb{Z}.\)
Vậy vào thời điểm \(t = - 1 + 3k,k \in \mathbb{Z}\) thì khoảng cách \(h\) là \(3\) m.
Khoảng cách \(h\) là \(0\) m khi
\(3\cos \left[ {\frac{\pi }{3}(2t - 1)} \right] = 0 \Leftrightarrow \cos \left[ {\frac{\pi }{3}(2t - 1)} \right] = 0 \Leftrightarrow \frac{\pi }{3}(2t - 1) = \frac{\pi }{2} + k\pi \Leftrightarrow t = \frac{5}{4} + \frac{3}{2}k,k \in \mathbb{Z}.\)
Vậy vào thời điểm \(t = \frac{5}{4} + \frac{3}{2}k,k \in \mathbb{Z}\) thì khoảng cách \(h\) là \(0\) m.
Lời giải
Số giờ nắng gắt trong ngày thứ \[n\] được tính bởi công thức: \(f\left( n \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {n - 80} \right)} \right] + 12\)
Vậy Tỉnh Quảng Nam chịu nhiều giờ nắng gắt nhất nghĩa là \(f\left( n \right)\) đạt giá trị lớn nhất
Ta có: \( - 1 \le \sin \left[ {\frac{\pi }{{182}}\left( {n - 80} \right)} \right] \le 1,\,\forall n\) \( \Rightarrow f\left( n \right) \le 15\)
Suy ra \(\max f\left( n \right) = 15 \Leftrightarrow \sin \left[ {\frac{\pi }{{182}}\left( {n - 80} \right)} \right] = 1\)
\( \Leftrightarrow \frac{\pi }{{182}}\left( {n - 80} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow n = 171 + k.364,\forall k \in \mathbb{Z}\)
Mà \(0 < n \le 365\) nên \(n = 171\).
Đán án: 171
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Tứ giác.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.