Lợi nhuận tổng hàng ngày (tính theo đô la) mà TKK Corporation thu được từ việc sản xuất và bán \(x\) đĩa DVD có thể ghi lại được cho bởi hàm lợi nhuận \(P(x) = - 0,000001{x^3} + 0,001{x^2} + 5x - 500;\quad 0 \le x \le 2000\). Tìm mức sản xuất \(x\) để lợi nhuận hàng ngày đạt cực đại. (làm tròn kết quả đến hàng đơn vị)

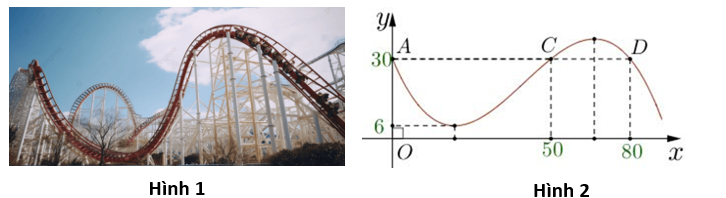
Dựa vào hình 2 ta thấy đồ thị hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\,\,\left( {a < 0} \right)\) và đường thẳng \(y = 30\) cắt nhau tại 3 điểm phân biệt có hoành độ \(x = 0;x = 50;x = 80.\)

\( \Rightarrow a{x^3} + b{x^2} + cx + d\, = 30 \Leftrightarrow a{x^3} + b{x^2} + cx + d - 30 = 0\)có 3 nghiệm phân biệt \(x = 0;x = 50;x = 80.\)

\( \Rightarrow a{x^3} + b{x^2} + cx + d - 30 = ax\left( {x - 50} \right)\left( {x - 80} \right) = a\left( {{x^3} - 130{x^2} + 4000x} \right)\)

Suy ra \(f\left( x \right) = a\left( {{x^3} - 130{x^2} + 4000x} \right) + 30\) \( \Rightarrow f'\left( x \right) = a\left( {3{x^2} - 260x + 4000} \right)\)

\(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 20\,\,\left( {TM} \right)}\\{x = \frac{{200}}{3}\,\left( {TM} \right)}\end{array}} \right.\).

Theo bài ra độ cao nhỏ nhất bằng 6 hay \(f\left( {20} \right) = 6 \Leftrightarrow a =  - \frac{1}{{1500}}\)

Độ cao lớn nhất mà tàu lượn siêu tốc đạt được là \(f\left( {\frac{{200}}{3}} \right) = \frac{{3230}}{{81}} \approx 39,9.\)

(a)  \(\overrightarrow {AB}  = (1 - 4; - 1 - 2;2 + 1) = ( - 3; - 3;3)\)

(b) \(\overrightarrow {AB}  = (1 - 4; - 1 - 2;2 + 1) = ( - 3; - 3;3) \Rightarrow |\overrightarrow {AB} | = \sqrt {{{( - 3)}^2} + {{( - 3)}^2} + {3^2}}  = 3\sqrt 3 \)

(c) Gọi \(M(x;y;z)\) thì \(\overrightarrow {MC}  = ( - x; - 2 - y,3 - z)\).

\({\rm{ V\`i  }}\overrightarrow {AB}  + \overrightarrow {CM}  = \vec 0 \Rightarrow \overrightarrow {AB}  = \overrightarrow {MC}  \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ - x =  - 3}\\{ - 2 - y =  - 3}\\{3 - z = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\\{z = 0}\end{array}} \right..{\rm{ }} \Rightarrow {\rm{M(3; }}1;0)} \right.{\rm{. }}\)

(d) Vì \[N\] thuộc mặt phẳng \[\left( {Oxy} \right)\] nên tọa độ điểm \[N\] là \(N(x;y;0)\)

Тa có: \(\overrightarrow {AN} (x - 4;y - 2;1);\overrightarrow {BN} (x - 1;y + 1; - 2)\)

Để \(A,B,N\) thẳng hàng thì hai vectơ \(\overrightarrow {AN} ,\overrightarrow {BN} \) cùng phương. Do đó, \(\overrightarrow {AN}  = k\overrightarrow {BN} \) (với \(k\) là số thực bất kì)

Suy ra, \(\left\{ {\begin{array}{*{20}{l}}{x - 4 = k(x - 1)}\\{y - 2 = k(y + 1)}\\{1 =  - 2k}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x - 4 =  - \frac{1}{2}(x - 1)}\\{y - 2 =  - \frac{1}{2}(y + 1)}\\{k = \frac{{ - 1}}{2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\end{array}} \right.} \right.} \right.\). Vậy \[N\left( {3;1;0} \right)\]