Trong không gian với hệ tọa độ Oxyz, cho ba điểm \[A\left( { - 2;3;1} \right)\], \[B\left( {2;1;0} \right)\], \[C\left( { - 3; - 1;1} \right)\]. Tìm tất cả các điểm \[D\] sao cho \[ABCD\] là hình thang có đáy \[AD\] và \[{S_{ABCD}} = 3{S_{ABC}}\].              

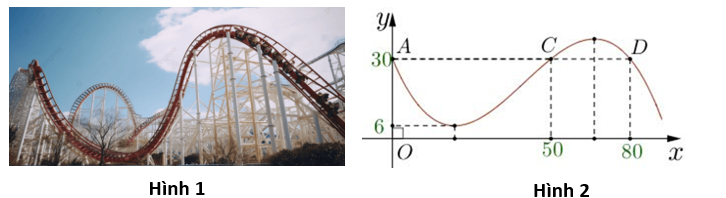
Dựa vào hình 2 ta thấy đồ thị hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\,\,\left( {a < 0} \right)\) và đường thẳng \(y = 30\) cắt nhau tại 3 điểm phân biệt có hoành độ \(x = 0;x = 50;x = 80.\)

\( \Rightarrow a{x^3} + b{x^2} + cx + d\, = 30 \Leftrightarrow a{x^3} + b{x^2} + cx + d - 30 = 0\)có 3 nghiệm phân biệt \(x = 0;x = 50;x = 80.\)

\( \Rightarrow a{x^3} + b{x^2} + cx + d - 30 = ax\left( {x - 50} \right)\left( {x - 80} \right) = a\left( {{x^3} - 130{x^2} + 4000x} \right)\)

Suy ra \(f\left( x \right) = a\left( {{x^3} - 130{x^2} + 4000x} \right) + 30\) \( \Rightarrow f'\left( x \right) = a\left( {3{x^2} - 260x + 4000} \right)\)

\(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 20\,\,\left( {TM} \right)}\\{x = \frac{{200}}{3}\,\left( {TM} \right)}\end{array}} \right.\).

Theo bài ra độ cao nhỏ nhất bằng 6 hay \(f\left( {20} \right) = 6 \Leftrightarrow a =  - \frac{1}{{1500}}\)

Độ cao lớn nhất mà tàu lượn siêu tốc đạt được là \(f\left( {\frac{{200}}{3}} \right) = \frac{{3230}}{{81}} \approx 39,9.\)

(a)  \(\overrightarrow {AB}  = (1 - 4; - 1 - 2;2 + 1) = ( - 3; - 3;3)\)

(b) \(\overrightarrow {AB}  = (1 - 4; - 1 - 2;2 + 1) = ( - 3; - 3;3) \Rightarrow |\overrightarrow {AB} | = \sqrt {{{( - 3)}^2} + {{( - 3)}^2} + {3^2}}  = 3\sqrt 3 \)

(c) Gọi \(M(x;y;z)\) thì \(\overrightarrow {MC}  = ( - x; - 2 - y,3 - z)\).

\({\rm{ V\`i  }}\overrightarrow {AB}  + \overrightarrow {CM}  = \vec 0 \Rightarrow \overrightarrow {AB}  = \overrightarrow {MC}  \Rightarrow \left\{ {\begin{array}{*{20}{l}}{ - x =  - 3}\\{ - 2 - y =  - 3}\\{3 - z = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\\{z = 0}\end{array}} \right..{\rm{ }} \Rightarrow {\rm{M(3; }}1;0)} \right.{\rm{. }}\)

(d) Vì \[N\] thuộc mặt phẳng \[\left( {Oxy} \right)\] nên tọa độ điểm \[N\] là \(N(x;y;0)\)

Тa có: \(\overrightarrow {AN} (x - 4;y - 2;1);\overrightarrow {BN} (x - 1;y + 1; - 2)\)

Để \(A,B,N\) thẳng hàng thì hai vectơ \(\overrightarrow {AN} ,\overrightarrow {BN} \) cùng phương. Do đó, \(\overrightarrow {AN}  = k\overrightarrow {BN} \) (với \(k\) là số thực bất kì)

Suy ra, \(\left\{ {\begin{array}{*{20}{l}}{x - 4 = k(x - 1)}\\{y - 2 = k(y + 1)}\\{1 =  - 2k}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x - 4 =  - \frac{1}{2}(x - 1)}\\{y - 2 =  - \frac{1}{2}(y + 1)}\\{k = \frac{{ - 1}}{2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 1}\end{array}} \right.} \right.} \right.\). Vậy \[N\left( {3;1;0} \right)\]