Trong không gian với hệ tọa độ Oxyz, cho \(\overrightarrow {OA} = 3\overrightarrow i + \overrightarrow j - 2\overrightarrow k \) và \(B\left( {m;m - 1; - 4} \right)\). Tìm tất cả giá trị của tham số \(m\)để độ dài đoạn \(AB = 3\).
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
\(\overrightarrow {OA} = 3\overrightarrow i + \overrightarrow j - 2\overrightarrow k \Rightarrow A\left( {3;1; - 2} \right)\)
\(AB = \sqrt {{{\left( {m - 3} \right)}^2} + {{\left( {m - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt {2{m^2} - 10m + 17} \).
\(AB = 3 \Leftrightarrow \sqrt {2{m^2} - 10m + 17} = 3 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = 4\end{array} \right.\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
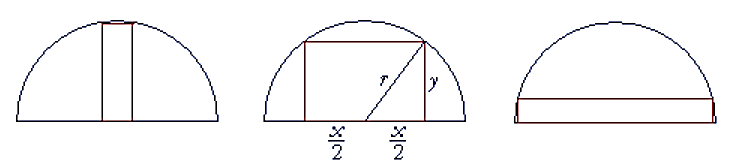
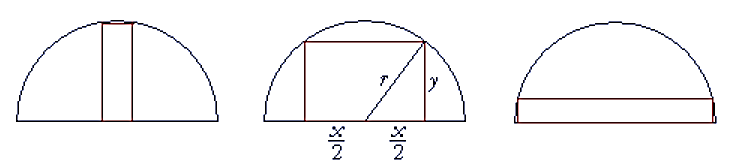
Ký hiệu các kích thước của hình chữ nhật như hình vẽ.
Ta có \({\left( {\frac{x}{2}} \right)^2} + {y^2} = {r^2}\) \( \Rightarrow {y^2} = {r^2} - \frac{{{x^2}}}{4} = 9 - \frac{{{x^2}}}{4}\). ĐK: \(0 < x < 6\).
Diện tích của tấm biển hình chữ nhật là \(S = xy\).
Ta có \({S^2} = {x^2}{y^2}\)\( = {x^2}\left( {9 - \frac{{{x^2}}}{4}} \right)\) \( = - \frac{1}{4}{x^4} + 9{x^2}\)\( = f\left( x \right)\).
\(f'\left( x \right) = - {x^3} + 18x\); \(f'\left( x \right) = 0 \Leftrightarrow x = 3\sqrt 2 \).
BBT:
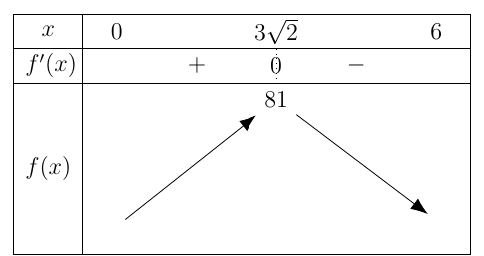
Suy ra \({S^2} \le 81\). Hay \(\max S = 9\), đạt được khi \(x = 3\sqrt 2 \) và \(y = \frac{3}{{\sqrt 2 }}\).
Khi đó, chiều dài của hình chữ nhật là \(x = 3\sqrt 2 \approx 4,24\).
Câu 2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một công ty bất động sản có \[150\] căn hộ cho thuê, biết rằng nếu cho thuê mỗi căn hộ với giá\[2\]triệu đồng mỗi tháng thì mỗi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm \[100.000\] đồng mỗi tháng thì có thêm \[5\] căn hộ bị bỏ trống. Mệnh đề nào sau đây đúng
a) Thu nhập cao nhất của công ty đạt được là 312.500.000 đồng.
b) Khi giá cho thuê mỗi căn hộ là 2.200.000 đồng thì có 10 căn hộ bị trống
c) Khi thu nhập công ty cao nhất thì số căn hộ có người thuê là 125 căn hộ.
d) Khi giá cho thuê mỗi căn hộ là 2.700.000 đồng thì thu nhập của công ty cao nhất.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Một công ty bất động sản có \[150\] căn hộ cho thuê, biết rằng nếu cho thuê mỗi căn hộ với giá\[2\]triệu đồng mỗi tháng thì mỗi căn hộ đều có người thuê và cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm \[100.000\] đồng mỗi tháng thì có thêm \[5\] căn hộ bị bỏ trống. Mệnh đề nào sau đây đúnga) Thu nhập cao nhất của công ty đạt được là 312.500.000 đồng.
b) Khi giá cho thuê mỗi căn hộ là 2.200.000 đồng thì có 10 căn hộ bị trống
c) Khi thu nhập công ty cao nhất thì số căn hộ có người thuê là 125 căn hộ.
d) Khi giá cho thuê mỗi căn hộ là 2.700.000 đồng thì thu nhập của công ty cao nhất.
Lời giải
|
a) |
Đ |
b) |
S |
c) |
Đ |
d) |
Đ |
Đúng; (b) Sai; (c) Đúng; (d) Đúng
Gọi số lần tăng giá tiền cho thuê mỗi căn hộ một tháng để công ty thu được thu nhập cao nhất là\[x\] (\(0 \le x \le 30\))
Số tiền cho thuê mỗi căn hộ là \[2 + 0,1x\]
Số căn hộ mỗi tháng được thuê là \[150 - 5x\]
Thu nhập của công ty đạt được là \[\left( {2 + 0,1x} \right)\left( {150 - 5x} \right)\]
Đặt\[f(x) = \left( {2 + 0,1x} \right)\left( {150 - 5x} \right)\]
\[\begin{array}{l}f'(x) = 0,1.\left( {150 - 5x} \right) - 5\left( {2 + 0,1x} \right) = 15 - 0,5x - 10 - 0,5x = 5 - x\\f'(x) = 0 \Leftrightarrow x = 5\end{array}\]
\(f\left( 0 \right) = 300;f(5) = 312,5;f(30) = 0\)\( \Rightarrow \mathop {Max}\limits_{x \in \left[ {0;30} \right]} f\left( x \right) = f\left( 5 \right) = 312,5\)khi\(x = 5\)
Vậy để có thu nhập cao nhất thì công ty đó phải cho thuê với giá \[2 + 0,1.5 = 2,5\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.