PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một bể ban đầu chứa 10 gal dung dịch muối với 2 lb muối. Dung dịch vào có nồng độ \(1.5lb/gal\) chảy vào với tốc độ \(3gal/\) phút, và hỗn hợp trong bể chảy ra với tốc độ \(4gal/\) phút. Người ta cho biết lượng muối trong bể sau \(t\) phút là \(x\) (pound), với\(x = f(t) = 1,5(10 - t) - 0,0013{(10 - t)^4},\quad 0 \le t \le 10.\)Hỏi lượng muối tối đa có thể có trong bể tại một thời điểm nào đó là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Một bể ban đầu chứa 10 gal dung dịch muối với 2 lb muối. Dung dịch vào có nồng độ \(1.5lb/gal\) chảy vào với tốc độ \(3gal/\) phút, và hỗn hợp trong bể chảy ra với tốc độ \(4gal/\) phút. Người ta cho biết lượng muối trong bể sau \(t\) phút là \(x\) (pound), với\(x = f(t) = 1,5(10 - t) - 0,0013{(10 - t)^4},\quad 0 \le t \le 10.\)Hỏi lượng muối tối đa có thể có trong bể tại một thời điểm nào đó là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Ta có công thức lượng muối \(x\) (pound) trong bể sau \(t\) phút:
\(x(t) = 1,5(10 - t) - 0,0013{(10 - t)^4};\quad 0 \le t \le 10\)
Đặt \(u = 10 - t\). Khi \(t\) chạy từ 0 đến 10 thì \(u\) chạy từ 10 xuống 0.
Khi đó \(x = 1,5u - 0,0013{u^4};\quad 0 \le u \le 10\)
Tính đạo hàm theo \(u\) ta được: \(1,5 - 0,0013 \cdot 4{u^3} = 1,5 - 0,0052{u^3}\)
Xét \(1,5 - 0,0052{u^3} = 0 \Rightarrow {u^3} = \frac{{1,5}}{{0,0052}} \approx 288,46 \Rightarrow u \approx \sqrt[3]{{288,46}} \approx 6,62\)
Lập bảng xét dấu ta được:
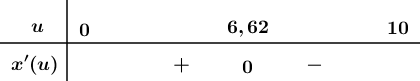
Suy ra tại \(u \approx 6,62\):
Lượng muối trong bể đạt tối đa khoảng 7,43 lb tại thời điểm \(t \approx 3,38\) phút kể từ lúc bắt đầu.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
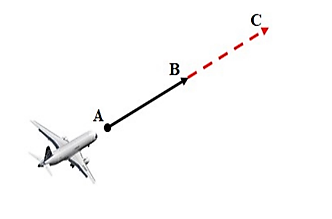
Do chiếc may bay di duyển với tốc độ và hướng không đổi từ \(A\) đến \(B\) trong 10 phút và từ \(B\) đến \(C\) trong 10 phút.
Nên suy ra \(AB = BC\) và \(A,\,B,\,C\) thẳng hàng.
Suy ra \(B\) là trung điểm của \(AC\)
\( \Rightarrow \left\{ \begin{array}{l}{x_B} = \frac{{{x_A} + {x_C}}}{2}\\{y_B} = \frac{{{y_A} + {y_C}}}{2}\\{z_B} = \frac{{{z_A} + {z_C}}}{2}\end{array} \right.\)\[ \Leftrightarrow \left\{ \begin{array}{l}950 = \frac{{812 + x}}{2}\\530 = \frac{{600 + y}}{2}\\6 = \frac{{5 + z}}{2}\end{array} \right.\]\( \Leftrightarrow \left\{ \begin{array}{l}x = 1088\\y = 460\\z = 7\end{array} \right.\).
Vậy \(x + y + z = 1555\).
Lời giải
Ta có doanh thu của doanh nghiệp khi bán \(x\) máy tính bảng là: \(D\left( x \right) = x.p\left( x \right) = x\left( {4000 - 10x} \right) = 4000x - 10{x^2}\).
Chi phí của doanh nghiệp để sản xuất \(x\) máy tính bảng là: \(C\left( x \right) = x.c\left( x \right) = x\left( {{x^2} - 70x + 400 + \frac{{1000}}{x}} \right) = {x^3} - 70{x^2} + 400x + 1000\).
Lợi nhuận của doanh nghiệp khi bán \(x\) máy tính bảng là: \(L\left( x \right) = D\left( x \right) - C\left( x \right) = 4000x - 10{x^2} - \left( {{x^3} - 70{x^2} + 400x + 1000} \right)\)\( = - {x^3} + 60{x^2} + 3600x - 1000\).
Xét hàm \(L\left( x \right) = - {x^3} + 60{x^2} + 3600x - 1000\left( {1 \le x \le 200;x \in \mathbb{N}} \right)\).
Có \(y' = - 3{x^2} + 120x + 3600\).
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 60\,\,\,\,\,\,\left( N \right)\\x = - 20\,\,\,\left( L \right)\end{array} \right.\).
Ta có bảng biến thiên
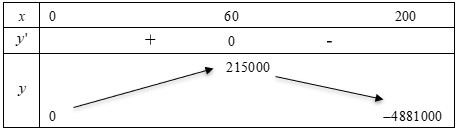
Dựa vào bảng biến thiên ta thấy doanh nghiệp đó sẽ bán \(60\) máy tính bảng để lợi nhuận cao nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.