Bộ 20 đề thi Giữa kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 7
34 người thi tuần này 4.6 3.5 K lượt thi 22 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 3
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 2
Đề kiểm tra Công thức xác suất toàn phần – công thức Bayes (có lời giải) - Đề 1
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 3
Đề kiểm tra Xác suất có điều kiện (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
Lời giải
Chọn A
Ta chứng minh \[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\sin \left( {\vec u,\,\vec v} \right)\].
Giả sử \[\vec u = \left( {{u_1};\,{u_2};\,{u_3}} \right)\] và \[\vec v = \left( {{v_1};\,{v_2};\,{v_3}} \right)\].
+) Nếu một trong hai vectơ \[\vec u\] và \[\,\vec v\] là vectơ \[\vec 0\] thì ta có \[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\sin \left( {\vec u,\,\vec v} \right)\].
+) Nếu cả hai vectơ \[\vec u\] và \[\,\vec v\] đều khác vectơ \[\vec 0\]. Khi đó ta có
\[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\sin \left( {\vec u,\,\vec v} \right)\]\[ = \left| {\vec u} \right|\left| {\vec v} \right|.\sqrt {1 - {{\cos }^2}\left( {\vec u,\,\vec v} \right)} \]\[ = \left| {\vec u} \right|\left| {\vec v} \right|.\sqrt {1 - \frac{{{{\left( {\vec u.\,\vec v} \right)}^2}}}{{{{\left| {\vec u} \right|}^2}.{{\left| {\vec v} \right|}^2}}}} \]\[ = \sqrt {{{\vec u}^2}.{{\vec v}^2} - {{\left( {\vec u.\,\vec v} \right)}^2}} \]\[ = \sqrt {{{\left( {{u_2}{v_3} - {v_2}{u_3}} \right)}^2} + {{\left( {{u_3}{v_1} - {v_3}{u_1}} \right)}^2} + {{\left( {{u_1}{v_2} - {v_1}{u_2}} \right)}^2}} \]\[ = \left| {\left[ {\vec u,\vec v} \right]} \right|\].
Ta có \[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\sin \left( {\vec u,\,\vec v} \right)\] nên khẳng định C sai.
Câu 2
Lời giải
Chọn B
\(\overrightarrow u .\overrightarrow v \)\( = x.1 + 2\left( { - 1} \right) + 1.2x\)\( = 3x - 2\).
Câu 3
Lời giải
Chọn B
Tọa độ điểm \(M'\) là điểm đối xứng của điểm \(M\left( {1;2;3} \right)\) qua gốc tọa độ \(O\) là \(M'\left( { - 1; - 2; - 3} \right)\).
Phương án nhiễu A: Học sinh nhầm:
Điểm \[M'\] là điểm đối xứng của điểm \[M(3;2;1)\] qua mặt phẳng \[(Oyz)\]\( \Rightarrow M'\left( { - 1;2;3} \right)\).
Phương án nhiễu B: Học sinh nhầm:
Điểm \[M'\] là điểm đối xứng của điểm \[M(3;2;1)\] qua trục \[Oz\]\( \Rightarrow M'\left( { - 1; - 2;3} \right)\).
Phương án nhiễu D: Học sinh nhầm:
Điểm \[M'\] là điểm đối xứng của điểm \[M(3;2;1)\] qua mặt phẳng \[(Oxy)\]\( \Rightarrow M'\left( {1;2; - 3} \right)\).
Câu 4
Lời giải
Chọn A
Ta có
\[y = \frac{{x + 1}}{{2 - x}} = \frac{{x + 1}}{{ - x + 2}} \Rightarrow y' = \frac{3}{{{{\left( { - x + 2} \right)}^2}}} > 0,{\rm{ }}\forall x \ne 2.\]
Do đó hàm số đã cho đồng biến trên các khoảng \[\left( { - \infty ;2} \right)\] và \[\left( {2; + \infty } \right)\].
Câu 5
Lời giải
Chọn A
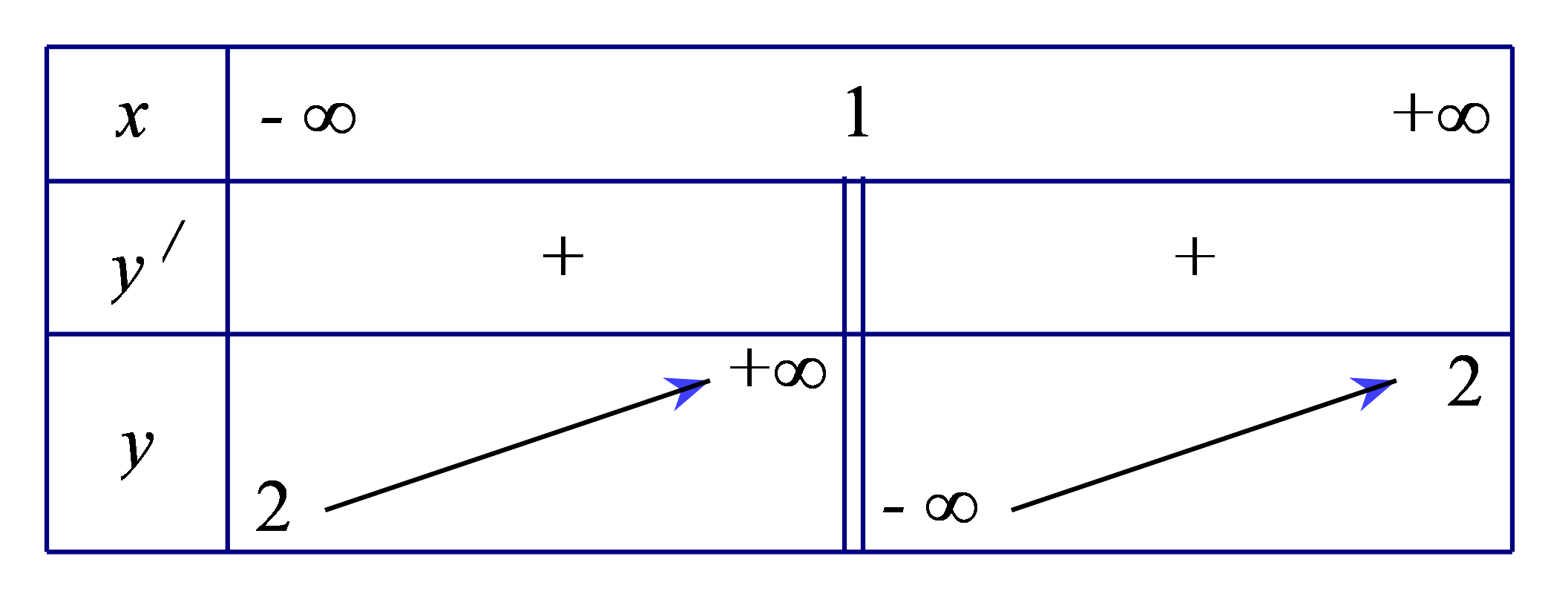
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x - 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 + \frac{1}{x}}}{{1 - \frac{2}{x}}} = 1\), tương tự \(\mathop {\lim }\limits_{x \to - \infty } y = 1\). Do vậy đồ thị hàm số có một đường tiệm cận ngang là \(y = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
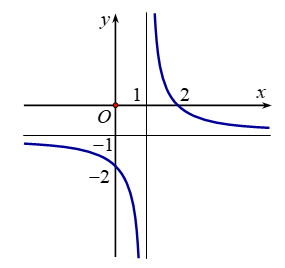
A. \(y = \frac{{ - 2x + 3}}{{1 - x}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.