PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Trong các khẳng định sau, khẳng định nào sai ?
A. \[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\cos \left( {\vec u,\,\vec v} \right)\].
B. \[\left[ {\vec u,\vec v} \right] = \vec 0\] \[ \Leftrightarrow \]\[\vec u\], \[\vec v\] cùng phương.
C. Nếu \[\vec u\], \[\vec v\] không cùng phương thì giá của vectơ \[\left[ {\vec u,\vec v} \right]\] vuông góc với mọi mặt phẳng song song với giá của các vectơ \[\vec u\] và \[\,\vec v\].
D. \[\left[ {\vec u,\vec v} \right].\,\vec u = \left[ {\vec u,\vec v} \right].\,\vec v = \vec 0\].
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
Ta chứng minh \[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\sin \left( {\vec u,\,\vec v} \right)\].
Giả sử \[\vec u = \left( {{u_1};\,{u_2};\,{u_3}} \right)\] và \[\vec v = \left( {{v_1};\,{v_2};\,{v_3}} \right)\].
+) Nếu một trong hai vectơ \[\vec u\] và \[\,\vec v\] là vectơ \[\vec 0\] thì ta có \[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\sin \left( {\vec u,\,\vec v} \right)\].
+) Nếu cả hai vectơ \[\vec u\] và \[\,\vec v\] đều khác vectơ \[\vec 0\]. Khi đó ta có
\[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\sin \left( {\vec u,\,\vec v} \right)\]\[ = \left| {\vec u} \right|\left| {\vec v} \right|.\sqrt {1 - {{\cos }^2}\left( {\vec u,\,\vec v} \right)} \]\[ = \left| {\vec u} \right|\left| {\vec v} \right|.\sqrt {1 - \frac{{{{\left( {\vec u.\,\vec v} \right)}^2}}}{{{{\left| {\vec u} \right|}^2}.{{\left| {\vec v} \right|}^2}}}} \]\[ = \sqrt {{{\vec u}^2}.{{\vec v}^2} - {{\left( {\vec u.\,\vec v} \right)}^2}} \]\[ = \sqrt {{{\left( {{u_2}{v_3} - {v_2}{u_3}} \right)}^2} + {{\left( {{u_3}{v_1} - {v_3}{u_1}} \right)}^2} + {{\left( {{u_1}{v_2} - {v_1}{u_2}} \right)}^2}} \]\[ = \left| {\left[ {\vec u,\vec v} \right]} \right|\].
Ta có \[\left| {\left[ {\vec u,\vec v} \right]} \right| = \left| {\vec u} \right|\left| {\vec v} \right|.\sin \left( {\vec u,\,\vec v} \right)\] nên khẳng định C sai.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
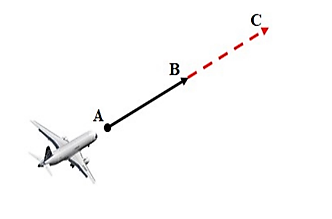
Do chiếc may bay di duyển với tốc độ và hướng không đổi từ \(A\) đến \(B\) trong 10 phút và từ \(B\) đến \(C\) trong 10 phút.
Nên suy ra \(AB = BC\) và \(A,\,B,\,C\) thẳng hàng.
Suy ra \(B\) là trung điểm của \(AC\)
\( \Rightarrow \left\{ \begin{array}{l}{x_B} = \frac{{{x_A} + {x_C}}}{2}\\{y_B} = \frac{{{y_A} + {y_C}}}{2}\\{z_B} = \frac{{{z_A} + {z_C}}}{2}\end{array} \right.\)\[ \Leftrightarrow \left\{ \begin{array}{l}950 = \frac{{812 + x}}{2}\\530 = \frac{{600 + y}}{2}\\6 = \frac{{5 + z}}{2}\end{array} \right.\]\( \Leftrightarrow \left\{ \begin{array}{l}x = 1088\\y = 460\\z = 7\end{array} \right.\).
Vậy \(x + y + z = 1555\).
Lời giải
Ta có doanh thu của doanh nghiệp khi bán \(x\) máy tính bảng là: \(D\left( x \right) = x.p\left( x \right) = x\left( {4000 - 10x} \right) = 4000x - 10{x^2}\).
Chi phí của doanh nghiệp để sản xuất \(x\) máy tính bảng là: \(C\left( x \right) = x.c\left( x \right) = x\left( {{x^2} - 70x + 400 + \frac{{1000}}{x}} \right) = {x^3} - 70{x^2} + 400x + 1000\).
Lợi nhuận của doanh nghiệp khi bán \(x\) máy tính bảng là: \(L\left( x \right) = D\left( x \right) - C\left( x \right) = 4000x - 10{x^2} - \left( {{x^3} - 70{x^2} + 400x + 1000} \right)\)\( = - {x^3} + 60{x^2} + 3600x - 1000\).
Xét hàm \(L\left( x \right) = - {x^3} + 60{x^2} + 3600x - 1000\left( {1 \le x \le 200;x \in \mathbb{N}} \right)\).
Có \(y' = - 3{x^2} + 120x + 3600\).
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 60\,\,\,\,\,\,\left( N \right)\\x = - 20\,\,\,\left( L \right)\end{array} \right.\).
Ta có bảng biến thiên
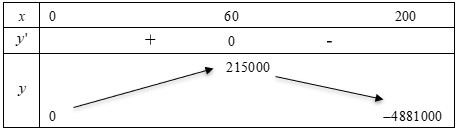
Dựa vào bảng biến thiên ta thấy doanh nghiệp đó sẽ bán \(60\) máy tính bảng để lợi nhuận cao nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập