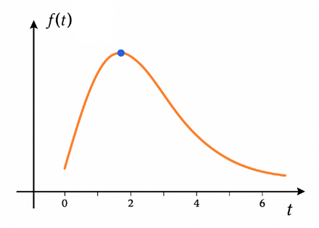
Một bể chứa 3000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 40 gam muối cho mỗi lít nước vởi tốc độ 30 lít/phút. Gọi \(f\left( t \right)\) là nồng độ muối trong bể sau \(t\) phút. khi \(t\) càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức \(x\) (gam/lít). Tính \(x\) (làm tròn đến hàng đơn vị)

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Lát cắt ngang của một vùng đất ven biển được mô hình hoá thành một hàm số bậc ba \[y = f\left( x \right)\] có đồ thị như hình vẽ (đơn vị độ dài trên các trục là km).

Biết khoảng cách hai bên chân đồi \(OA = 2\,\,{\rm{km}}\), độ rộng của hồ \(AB = 1\,\,{\rm{km}}\) và ngọn đồi cao \[528\,\,{\rm{m}}\]. Tìm độ sâu của hồ (tính bằng mét) tại điểm sâu nhất? (làm tròn đến hàng đơn vị).

Doanh số bán hàng của một loại sản phẩm (chục triệu đồng) trong một phiên livestream bán hàng kéo dài sáu giờ theo quy luật hàm số \(f(t) = \frac{{3t}}{{{e^{\frac{t}{2}}}}},0 \le t \le 6\) trong đó thời gian \(t\) được tính bằng giờ kể từ khi bắt đầu livestream.

Khi đó, đạo hàm \(f\prime (t)\) sẽ biểu thị tốc độ bán hàng. Hỏi sau bao nhiêu giờ kể từ khi bắt đầu phiên livestream thì doanh số bán hàng là lớn nhất?

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Cho hàm số \(y = f\left( x \right)\) có điểm cực tiểu \({x_1}\) và điểm cực đại \({x_2}\). Khi đó

              a) \(f\left( {{x_1}} \right),f\left( {{x_2}} \right)\)là các cực trị của hàm số \(y = f\left( x \right)\);

              b) \({x_1} < {x_2}\);

              c) \(f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).

              d) \({x_1}\)và \({x_2}\) là các điểm cực trị của hàm số \(y = f\left( x \right)\);

              a) Để đạt lợi nhuận lớn nhất thì sau khi tăng giá mỗi chiếc khăn lãi \[21000\] đồng.

              b) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần bán với giá \[39000\] đồng.

              c) Để đạt lợi nhuận lớn nhất thì mỗi chiếc khăn cần tăng thêm \[10000\] đồng.

              d) Để đạt lợi nhuận lớn nhất thì số khăn bán ra giảm \[800\] chiếc.