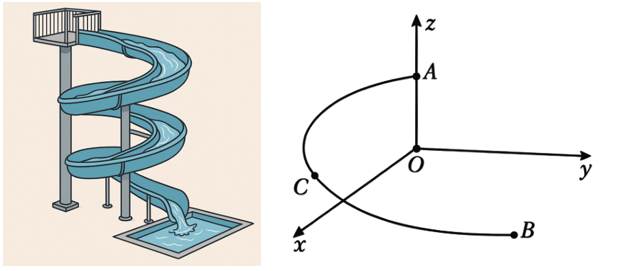
Trượt nước là một trò chơi vận động được nhiều người yêu thích trong các công viên nước. Một cái máng trượt nước có thiết kế dạng cung tròn với hai đầu mút là \(A\) và \(B\). Chọn hệ trục tọa độ \(Oxyz\) với gốc \(O\) đặt tại hình chiếu của \(A\) trên mặt đất, mặt phẳng \(\left( {Oxy} \right)\) trùng với mặt đất và trục \(Oz\) hướng thẳng đứng lên trời, đơn vị đo lấy theo mét (tham khảo hình vẽ dưới đây). Biết các điểm \(A,B\) và một điểm \(C\)nằm trên máng trượt lần lượt có tọa độ là \(\left( {0;0;5} \right),\left( {6;7;1} \right)\) và \(\left( {5;0;2} \right)\). Độ dài máng trượt nước đó bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị của mét)?
Câu hỏi trong đề: Bộ 20 đề thi Giữa kì 1 Toán 12 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
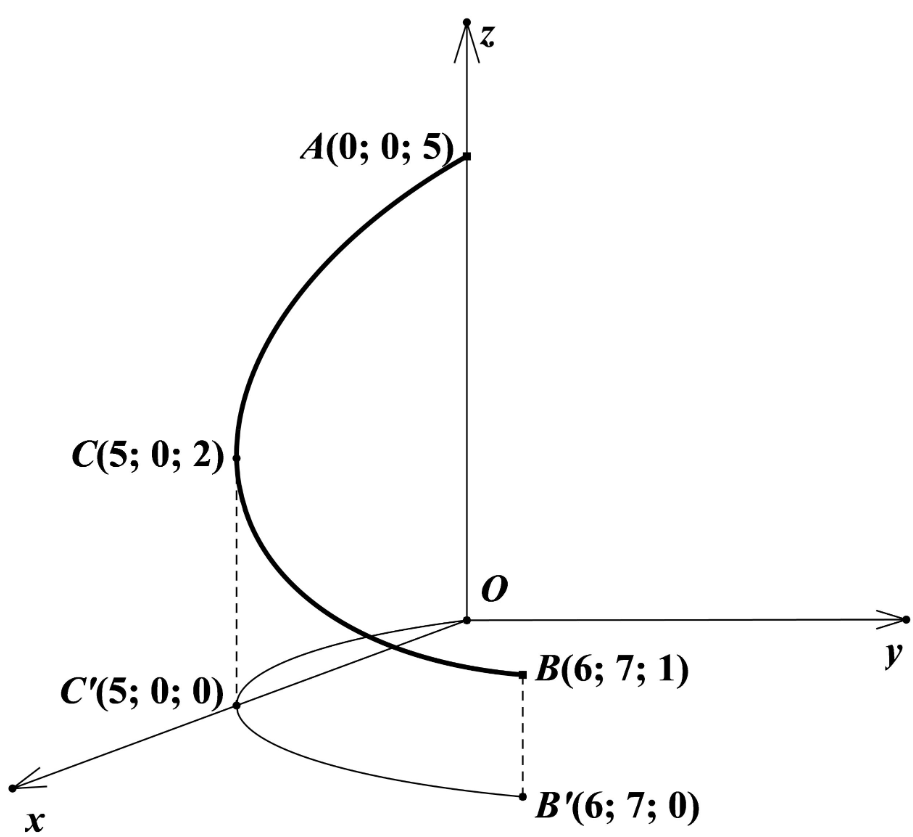
Ta có: \(A\left( {0;0;5} \right),B\left( {6;7;1} \right),C\left( {5;0;2} \right) \Rightarrow \overrightarrow {AB} = \left( {6;7; - 4} \right),\overrightarrow {AC} = \left( {5;0; - 3} \right),\overrightarrow {BC} = \left( { - 1; - 7;1} \right)\).
\(\left[ {\overrightarrow {AC} ,\overrightarrow {AB} } \right] = \left( {21;2;35} \right)\); \(AB = \sqrt {101} \); \(AC = \sqrt {34} \); \(BC = \sqrt {51} \).
\({S_{\Delta ABC}} = \frac{1}{2}\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {AB} } \right]} \right| = \frac{{\sqrt {{{21}^2} + {2^2} + {{35}^2}} }}{2} = \frac{{\sqrt {1670} }}{2}\).
Bán kính đường tròn ngoại tiếp tam giác \(ABC\) bằng: \(R = \frac{{AB.AC.BC}}{{4{S_{\Delta ABC}}}} = \frac{{\sqrt {101} .\sqrt {34} .\sqrt {51} }}{{4.\frac{{\sqrt {1670} }}{2}}} = \frac{{17\sqrt {253005} }}{{1670}} \approx 5,12\).
\(\cos \widehat C = \frac{{A{C^2} + B{C^2} - A{B^2}}}{{2.AC.BC}} = - \frac{{4\sqrt 6 }}{{51}}\). Suy ra \(\widehat C \approx 1,7641 \Rightarrow \widehat A + \widehat B \approx \pi - 1,7641 \approx 1,3775\).
Suy ra số đo cung \(ACB\) bằng \(2\left( {\widehat A + \widehat B} \right) \approx 2,755 = \alpha \)
Suy ra độ dài cung bằng \(R.\alpha \approx 14,1056 \approx 14\left( m \right)\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án:
Doanh thu khi nhà máy \(A\) bán hết \(x\) tấn sản phẩm cho nhà máy \(B\) là: \(x.P\left( x \right) = x\left( {45 - 0,001{x^2}} \right) = 45x - 0,001{x^3}\).
Lợi nhuận thu được là: \(L\left( x \right) = 45x - 0,001{x^3} - \left( {100 + 30x} \right)\)\( = - 0,001{x^3} + 15x - 100\).
Ta có: \(L'\left( x \right) = - 0,003{x^2} + 15 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x \approx 70,7\,\,\,}\\{x \approx - 70,7}\end{array}} \right.\)
Bảng biến thiên:
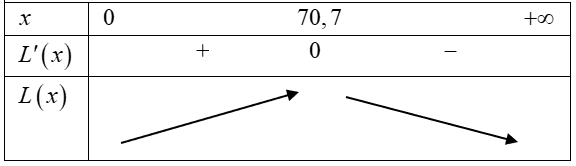
Ta có: \(L\left( {70} \right) = 607\), \(L\left( {71} \right) = 607,089 > L\left( {70} \right)\)
Như vậy, nhà máy \(A\) cần bán \(71\) tấn sản phẩm cho nhà máy \(B\) mỗi tháng để lợi nhuận thu được là lớn nhất.
Lời giải
Đáp án:
Gọi \[p\](triệu đồng) là giá của một máy điều hòa và \(x\) là số máy điều hòa bán ra trong tháng.
Ta có hàm cầu \[p = ax + b\] đi qua các điểm \(\left( {700;15} \right)\) và \(\left( {800;14} \right)\)
Suy ra \[p = - \frac{1}{{100}}x + 22\]
Ta có hàm doanh thu trong tháng là: \[R\left( x \right) = px = - \frac{1}{{100}}{x^2} + 22x\]
Suy ra hàm lợi nhuận của cửa hàng trong tháng là: \[\begin{array}{l}L\left( x \right) = R\left( x \right) - C\left( x \right) = - \frac{1}{{100}}{x^2} + 22x - \left( {14000 - 3x} \right)\\ \Leftrightarrow L\left( x \right) = - \frac{1}{{100}}{x^2} + 25x - 14000\end{array}\]
Ta có \[L\left( x \right)\] đạt GTLN bằng 1625 (triệu đồng) khi \(x = 1250\)
Vậy cửa hàng nên đặt giá bán để lợi nhuận lớn nhất là: \[p = - \frac{1}{{100}}.1250 + 22 = 9,5\] (triệu đồng)
Câu 3
a) Đồ thị \(\left( C \right)\) nhận giao điểm \(I\left( {3\,;\, - 9} \right)\) làm tâm đối xứng.
b) Đồ thị \(\left( C \right)\) có tiệm cận xiên là \(y = - x - 6\).
c) Đồ thị không cắt trục \(Ox\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) Đạo hàm của hàm số đã cho là \(y' = 3{x^2} - 6x\).
b) Hàm số đã cho đồng biến trên khoảng \(\left( {0;2} \right)\) và nghịch biến trên các khoảng \(\left( { - \infty ;0} \right),\left( {2; + \infty } \right)\).
c) Bảng biến thiên của hàm số đã cho là:
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
b) Gọi \(E\) là điểm đối xứng của điểm \(M\) qua \(N\). Tọa độ của điểm \(E\) là \(\left( { - 4; - 1;3} \right)\).
c) Hình chiếu của điểm \(M\) trên trục \(Oy\) có tọa độ là \(\left( { - 2;3;1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập