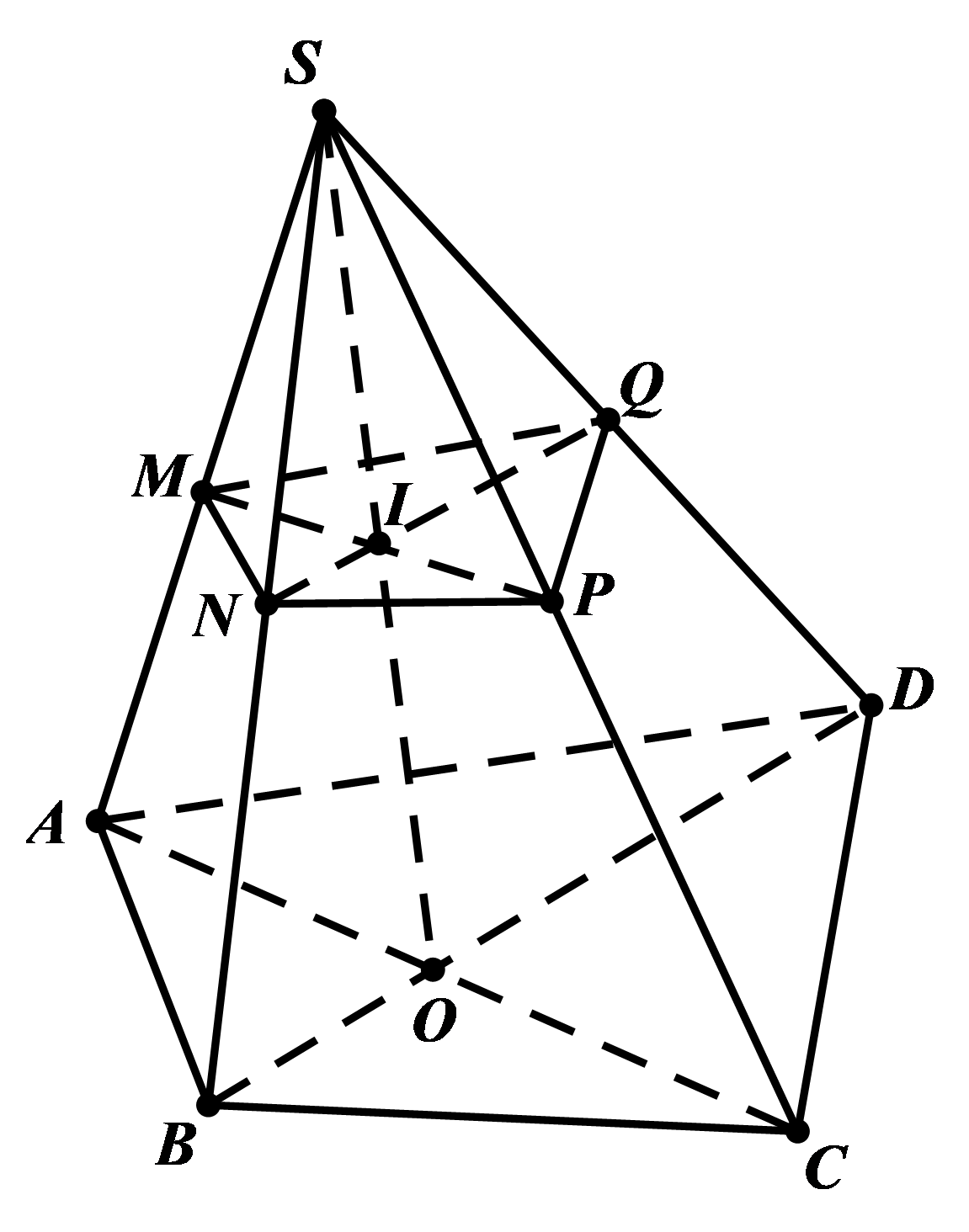Cho hình chóp tứ giác \[S.ABCD\], gọi \[O\] là giao điểm của hai đường chéo \[AC\] và \[BD\]. Một mặt phẳng \[\left( \alpha \right)\] cắt các cạnh bên \[SA,SB,SC,SD\] tương ứng tại các điểm \[M,N,P,Q\]. Khẳng định nào đúng?
Câu hỏi trong đề: Bộ 10 đề thi Giữa kì 1 Toán 10 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Lời giải
Đáp án đúng là: A
|
Trong mặt phẳng \[\left( {MNPQ} \right)\] gọi \[I = MP \cap NQ\]. Ta sẽ chứng minh \[I \in SO\]. Dễ thấy \[SO = \left( {SAC} \right) \cap \left( {SBD} \right)\]. \[\left\{ \begin{array}{l}I \in MP \subset \left( {SAC} \right)\\I \in NQ \subset \left( {SBD} \right)\end{array} \right.\] \[ \Rightarrow \left\{ \begin{array}{l}I \in \left( {SAC} \right)\\I \in \left( {SBD} \right)\end{array} \right. \Rightarrow I \in SO\] Vậy \[MP,NQ,SO\] đồng quy tại \[I\]. |
|
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
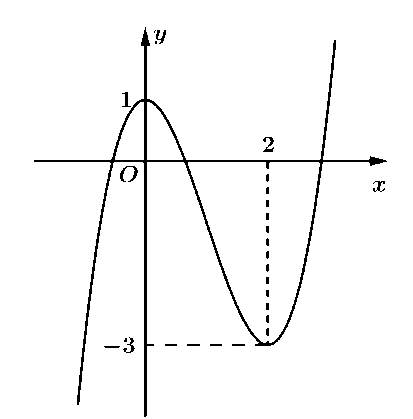
Từ đồ thị hàm số ta có
Trên khoảng \[\left( { - \infty ;0} \right)\], đồ thị hàm số đi lên từ trái sang phải nên hàm số đồng biến trên khoảng \[\left( { - \infty ;0} \right)\].
Trên khoảng \[\left( {0;2} \right)\], đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến trên khoảng \[\left( {0;2} \right)\].
Trên khoảng \[\left( {2; + \infty } \right)\], đồ thị hàm số đi lên từ trái sang phải nên hàm số đồng biến trên khoảng \[\left( {2; + \infty } \right)\].
Vậy khẳng định C đúng.
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: A
Với vectơ \(\overrightarrow a \) khác \(\overrightarrow 0 \) và một số thực \(k \ne 0\), ta có hai vectơ \(\overrightarrow a ,\,\,k\overrightarrow a \) luôn cùng phương với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.