Trong không gian \(Oxyz\), cho tam giác \(ABC\) với \(A\left( {1;0; - 2} \right),B\left( { - 2;3;4} \right),C\left( {4; - 6;1} \right)\).
a) \(\overrightarrow {AB} = \left( {3; - 3;6} \right)\).
b) Hình chiếu vuông góc của \(B\) lên trục \(Ox\) là \(B'\left( { - 2;3;0} \right)\).
c) Tồn tại 1 điểm \(M\) thuộc trục hoành sao cho tam giác \(MBC\) vuông tại \(M\).
d) Nếu \(ABDC\) là hình bình hành thì tọa độ điểm \(D\) là \(\left( {1; - 3;7} \right)\).
Quảng cáo
Trả lời:
a) Sai. Ta có \(\overrightarrow {AB} = \left( { - 3;3;6} \right)\).
b) Sai. Hình chiếu vuông góc của \(B\) lên trục \(Ox\) là \(B'\left( { - 2;0;0} \right)\).
c) Sai. Vì \(M\) thuộc trục hoành nên \(M\left( {m;0;0} \right)\).
Khi đó \(\overrightarrow {MB} = \left( { - 2 - m;3;4} \right),\overrightarrow {MC} = \left( {4 - m; - 6;1} \right)\).
Suy ra \(\overrightarrow {MB} \cdot \overrightarrow {MC} = \left( {m + 2} \right)\left( {m - 4} \right) - 18 + 4\).
Vì tam giác \(MBC\) vuông tại \(M\) nên \(\overrightarrow {MB} \cdot \overrightarrow {MC} = 0\)
\( \Rightarrow \left( {m + 2} \right)\left( {m - 4} \right) - 18 + 4 = 0 \Leftrightarrow m = 1 \pm \sqrt {23} \).
Như vậy tồn tại 2 điểm \(M\) thỏa mãn yêu cầu.
d) Đúng. Gọi \(D\left( {a;b;c} \right)\).
Vì \(ABDC\) là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {CD} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a - 4 = - 3}\\{b + 6 = 3}\\{c - 1 = 6}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = - 3}\\{c = 7}\end{array}} \right.} \right.\).
Vậy \(D\left( {1; - 3;7} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Radar đặt trên đỉnh tháp, trục \(Oz\) hướng thẳng đứng lên phía trên, suy ra tọa độ của đỉnh tháp \(E\left( {0\,;0\,;\,0,1} \right)\).
b) Đúng. Tọa độ điểm \(F\left( {400; - 300;12} \right)\).
\[\overrightarrow {EF} = \left( {400; - 300;11,9} \right) \Rightarrow EF \approx 500,14 < 600\,\,\left( {{\rm{km}}} \right)\].
Vậy \(F\) nằm trong phạm vi điều khiển của radar.
c) Sai. Từ \(F\), máy bay bay 1 giờ đến \(A\) với vận tốc \(900\,{\rm{km/h}}\) theo phương \(\overrightarrow a = \left( {3;4;0} \right)\).
Suy ra \[\left\{ \begin{array}{l}\overrightarrow {FA} = k\overrightarrow a \\\left| {\overrightarrow {FA} } \right| = 900\end{array} \right. \Rightarrow k\left| {\overrightarrow a } \right| = 900 \Rightarrow k = \frac{{900}}{{\sqrt {{3^2} + {4^2}} }} = 180.\]
Suy ra \(\overrightarrow {FA} = \left( {540;720;0} \right) \Rightarrow A\left( {940;420;12} \right).\)
d) Sai. Gọi \(K\left( {x;y;z} \right)\) là điểm máy bay đạt đến phạm vi quan sát của radar, suy ra \(EK = 600\).
Khi đó \(\overrightarrow {FK} = k\overrightarrow a \left( {k > 0} \right) \Leftrightarrow \left\{ \begin{array}{l}x - 400 = 3k\\y + 300 = 4k\\z - 12 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 400 + 3k\\y = - 300 + 4k\\z = 12\end{array} \right. \Rightarrow K\left( {400 + 3k; - 300 + 4k;12} \right)\).
Suy ra \(\overrightarrow {EK} = \left( {400 + 3k; - 300 + 4k;11,9} \right)\), mà \(EK = 600.\)
Nên \({\left( {400 + 3k} \right)^2} + {\left( { - 300 + 4k} \right)^2} + 11,{9^2} = {600^2} \Leftrightarrow 25{k^2} = 109858,39 \Leftrightarrow k \approx 66.\)
Khi đó \(K\left( {598; - 36;12} \right) \Rightarrow \overrightarrow {FK} = \left( {198;264;0} \right) \Rightarrow FK = 330\).
Thời gian máy bay trong phạm vi theo dõi của radar là \(t = \frac{{330 \cdot 60}}{{900}} = 22\) phút.
Lời giải
Bài toán này ta sẽ giải quyết bằng cách ứng dụng phương pháp tọa độ trong không gian.
Đặt hệ trục tọa độ như hình vẽ. Không mất tính tổng quát, và dựa vào yêu cầu về vị trí 3 con nhện ta xác định là các điểm \(M,N,P\) nằm trên các cạnh \[A'B',CC',AD\] như hình vẽ.
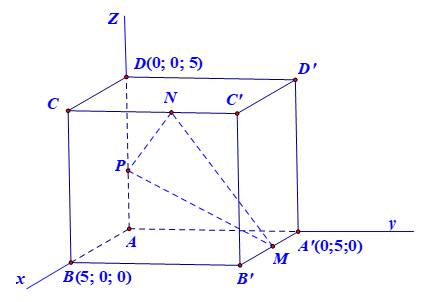
Yêu cầu bài toán là cần tìm tọa độ của 3 điểm \(M,N,P\) để chu vi tam giác \(MNP\) nhỏ nhất.
Đặt \[M\left( {x;5;0} \right),P\left( {0;0;z} \right),N\left( {5;y;5} \right)\]. Chu vi tam giác \[MNP\] là:
\[\begin{array}{l}MN + NP + PM = \sqrt {{{\left( {x - 5} \right)}^2} + {{\left( {y - 5} \right)}^2} + {5^2}} + \sqrt {{5^2} + {y^2} + {{\left( {z - 5} \right)}^2}} + \sqrt {{x^2} + {5^2} + {z^2}} \\ = \sqrt {{{\left( {5 - x} \right)}^2} + {{\left( {y - 5} \right)}^2} + {5^2}} + \sqrt {{y^2} + {{\left( {z - 5} \right)}^2} + {5^2}} + \sqrt {{z^2} + {{\left( { - x} \right)}^2} + {5^2}} .\end{array}\]
Áp dụng bất đẳng thức vectơ:
\[\begin{array}{l} \Rightarrow MN + NP + PM \ge \sqrt {{{\left( {5 - x + y} \right)}^2} + {{\left( {y + z - 10} \right)}^2} + {{10}^2}} + \sqrt {{z^2} + {{\left( { - x} \right)}^2} + {5^2}} \\ \ge \sqrt {{{\left( {5 - x + y + z} \right)}^2} + {{\left( {y - 5 + z - 5 - x} \right)}^2} + {{\left( {5 + 5 + 5} \right)}^2}} \\ = \sqrt {2{{\left( {y + z - x - \frac{5}{2}} \right)}^2} + \frac{{225}}{2} + {{\left( {5 + 5 + 5} \right)}^2}} \ge 15\sqrt {\frac{3}{2}} = 15\frac{{\sqrt 6 }}{2}.\end{array}\]
Dấu bằng xảy ra khi \[\left\{ \begin{array}{l}y + z - x = \frac{5}{2}\\\frac{{5 - x}}{y} = \frac{{y - 5}}{{z - 5}} = \frac{5}{5}\\\frac{{5 - x + y}}{z} = \frac{{y + z - 10}}{{ - x}} = \frac{{10}}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = z\\2y - x = \frac{5}{2}\\x + y = 5\end{array} \right. \Leftrightarrow x = y = z = \frac{5}{2}\].
Vậy giá trị cần tìm là \[\frac{{15}}{2}\sqrt 6 \] \( \Rightarrow {m^2} + {n^2} + {p^2} = 265.\)
Đáp án: 265.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.