Trong không gian \[Oxyz\], cho đường thẳng \(d:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z + 2}}{1}\) và mặt phẳng \(\left( P \right):3x - y + z - 25 = 0\). Một đường thẳng \(d'\) cắt trục \(Oz\) tại điểm \(M\), cắt đường thẳng \(d\) tại điểm \(N\) và \(d'\) song song với \(\left( P \right)\). Độ dài nhỏ nhất của đoạn \(MN\) bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \[M\left( {0\,;\,0\,;\,m} \right) \in Oz\], \[N\left( {1 + t\,;\,2t\,;\, - 2 + t} \right) \in d\]\[ \Rightarrow \overrightarrow {MN} = \left( {1 + t\,;\,2t\,;\, - 2 + t - m} \right)\].
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \[\overrightarrow n = \left( {3\,;\, - 1\,;\,1} \right)\].
Vì \(d'\) song song với \(\left( P \right)\) nên \[\overrightarrow {MN} \cdot \overrightarrow n = 0\]\[ \Leftrightarrow 3 + 3t - 2t - 2 + t - m = 0\]\[ \Leftrightarrow m = 2t + 1\].
\[ \Rightarrow \overrightarrow {MN} = \left( {1 + t\,;\,2t\,;\, - t - 3} \right)\]\[ \Rightarrow MN = \sqrt {{{\left( {1 + t} \right)}^2} + 4{t^2} + {{\left( { - t - 3} \right)}^2}} = \sqrt {6{t^2} + 8t + 10} \].
Độ dài đoạn \(MN\) nhỏ nhất \[ \Leftrightarrow \]\[t = - \frac{2}{3}\].
Đoạn dài nhỏ nhất của đoạn \(MN\) bằng \[\sqrt {\frac{{22}}{3}} = \frac{{\sqrt {66} }}{3} \approx 2,71\].
Đáp án: 2,71.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \[M = AB \cap CD\] (là điểm hai viên đạn va chạm nhau) khi đó \[AM = 150\,{\rm{m}}\;(1)\].
Ta có \[\overrightarrow {AB} = \left( {1\,;2\,;2} \right)\] là vectơ chỉ phương của đường thẳng \[AB\].
Phương trình tham số đường thẳng \[AB\] là \[\left\{ {\begin{array}{*{20}{c}}{x = 5 + t}\\{y = 7 + 2t}\\{z = 10 + 2t}\end{array}} \right.\quad (t \in \mathbb{R})\].
Do \[M \in AB \Rightarrow M\left( {5 + t;7 + 2t;10 + 2t} \right)\]. Từ (1) ta có \[\sqrt {{t^2} + 4{t^2} + 4{t^2}} = 150 \Leftrightarrow \left| t \right| = 50\].
Với \[t = 50 \Rightarrow M\left( {55;107;110} \right)\] và với \[t = - 50 \Rightarrow M\left( { - 45; - 93; - 90} \right)\].
Vì cao độ điểm \[D\] dương nên cao độ của điểm \[M\] dương\[ \Rightarrow M\left( {55\,;107\,;110} \right)\].
Vậy vectơ chỉ phương của đường thẳng \[CD\] là \[\overrightarrow {CM} = \left( {40;90;105} \right)\].
Khi đó, phương trình tham số đường thẳng \[CD\] là \[\left\{ {\begin{array}{*{20}{c}}{x = 15 + 40t'}\\{y = 17 + 90t'}\\{z = 5 + 105t'}\end{array}} \right.\quad (t' \in \mathbb{R})\].
Mà điểm \[D\] cách mặt đất \[26\,{\rm{m}}\] nên điểm \[D\] có cao độ bằng \[26\]
\[ \Rightarrow \]\[5 + 105t' = 26 \Leftrightarrow t' = \frac{1}{5} \Rightarrow D\left( {23\,;35\,;26} \right)\]. \[C\left( {15\,;17\,;5} \right)\]
Khi đó độ dài \[CD = \sqrt {{{\left( {15 - 23} \right)}^2} + {{\left( {17 - 35} \right)}^2} + {{\left( {5 - 26} \right)}^2}} \approx 28,8\,\,{\rm{(m)}}.\]
Đáp án: 28,8.
Lời giải
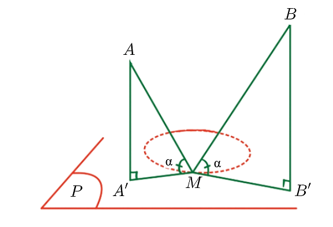
Gọi \(A',B'\) lần lượt là hình chiếu vuông góc của \(A,B\) lên mặt phẳng \(\left( P \right)\).
Góc tạo bởi \(MA\) với mặt vườn và góc tạo bởi \(MB\) với mặt vườn phải luôn bằng nhau.
Nên ta có \( \Rightarrow \frac{{MA}}{{MB}} = \frac{{AA'}}{{BB'}} = \frac{{d\left( {A,\left( P \right)} \right)}}{{d\left( {B,\left( P \right)} \right)}}\).
Mà \(d\left( {A,\left( P \right)} \right) = \frac{{\left| {2 \cdot 40 + 2 \cdot \left( { - 40} \right) - 12 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 8\); \[d\left( {B,\left( P \right)} \right) = \frac{{\left| {2 \cdot \left( { - 40} \right) + 2 \cdot 50 - 38 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 10\].
\( \Rightarrow \frac{{MA}}{{MB}} = \frac{8}{{10}} = \frac{4}{5} \Rightarrow 5MA = 4MB\). Gọi \(M\left( {x;y;z} \right)\). Khi đó, ta được:
\(25 \cdot \left[ {{{\left( {x - 40} \right)}^2} + {{\left( {y + 40} \right)}^2} + {{\left( {z - 12} \right)}^2}} \right] = 16 \cdot \left[ {{{\left( {x + 40} \right)}^2} + {{\left( {y - 50} \right)}^2} + {{\left( {z - 38} \right)}^2}} \right]\).
Rút gọn ta được phương trình mặt cầu \(\left( S \right)\) chứa các điểm \(M\) thoả mãn yêu cầu kĩ thuật:
\({x^2} + {y^2} + {z^2} - \frac{{3280}}{9}x + 400y + \frac{{616}}{9}z - \frac{{5104}}{9} = 0\).
Đồng thời, vì điểm \(M\) nằm trên mặt vườn nên \(M \in \left( P \right):\;{\mkern 1mu} 2x + 2y - z - 12 = 0\).
Như vậy, tập hợp điểm \(M\) cần tìm là giao tuyến của mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( P \right)\), tức là một đường tròn \(\left( C \right)\).
Gọi \(I\) là tâm mặt cầu \(\left( S \right)\), ta được: \(I\left( {\frac{{1640}}{9}; - 200; - \frac{{308}}{9}} \right)\).
Bán kính của mặt cầu \(\left( S \right)\):
\(R = \sqrt {{a^2} + {b^2} + {c^2} - d} = \sqrt {{{\left( {\frac{{1640}}{9}} \right)}^2} + {{\left( { - 200} \right)}^2} + {{\left( {\frac{{ - 308}}{9}} \right)}^2} + \frac{{5104}}{9}} = \sqrt {\frac{{6070400}}{{81}}} \).
Khoảng cách từ tâm \(I\) đến mặt phẳng \(\left( P \right)\): \(d = \frac{{\left| {2 \cdot \frac{{1640}}{9} + 2 \cdot \left( { - 200} \right) + \frac{{308}}{9} - 12} \right|}}{{\sqrt {4 + 4 + 1} }} = \frac{{40}}{9}\).
Bán kính đường tròn giao tuyến \(\left( C \right)\): \(r = \sqrt {{R^2} - {d^2}} = \sqrt {\frac{{6068800}}{{81}}} \).
Vậy độ dài đường ray là chu vi đường tròn \(\left( C \right)\): \(l = 2\pi r \approx 1720\;{\rm{(m)}}\).
Đáp án: 1720.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo