Hệ thống định vị vệ tinh toàn cầu Beidou (Bắc Đẩu) hiện tại có 35 vệ tinh, mỗi vệ tinh cách Trái Đất khoảng 35 000 km, ta coi Trái Đất là khối cầu có bán kính \(R = 6,4\) (nghìn km). Với hệ tọa độ \(Oxyz\) đã chọn, \(O\) là tâm Trái Đất và đơn vị trên mỗi trục là nghìn km, hai vệ tinh có tọa độ \(A\left( {30;0;0} \right),B\left( {0;30;0} \right)\). Xét điểm \(M\left( {x;y;z} \right)\) thuộc bề mặt Trái Đất. Đặt \(T\) là tổng khoảng cách từ \(M\) đến hai vệ tinh \(A\) và \(B\). Tìm giá trị nhỏ nhất của \(T\) theo đơn vị nghìn km (làm tròn kết quả đến hàng phần chục).
Hệ thống định vị vệ tinh toàn cầu Beidou (Bắc Đẩu) hiện tại có 35 vệ tinh, mỗi vệ tinh cách Trái Đất khoảng 35 000 km, ta coi Trái Đất là khối cầu có bán kính \(R = 6,4\) (nghìn km). Với hệ tọa độ \(Oxyz\) đã chọn, \(O\) là tâm Trái Đất và đơn vị trên mỗi trục là nghìn km, hai vệ tinh có tọa độ \(A\left( {30;0;0} \right),B\left( {0;30;0} \right)\). Xét điểm \(M\left( {x;y;z} \right)\) thuộc bề mặt Trái Đất. Đặt \(T\) là tổng khoảng cách từ \(M\) đến hai vệ tinh \(A\) và \(B\). Tìm giá trị nhỏ nhất của \(T\) theo đơn vị nghìn km (làm tròn kết quả đến hàng phần chục).
Quảng cáo
Trả lời:
Giải bởi Vietjack
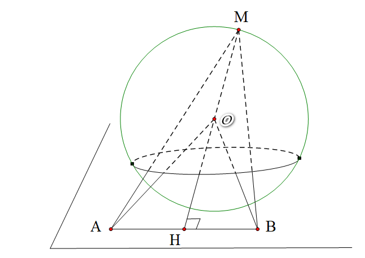
Mặt cầu \(\left( S \right)\) có tâm \(O\left( {0;0;0} \right)\) và bán kính \(R = 6,4\) có phương trình \({x^2} + {y^2} + {z^2} = 40,96\).
Ta có \(OA = 30;OB = 30;AB = 30\sqrt 2 \). Suy ra \(\Delta OAB\) cân tại \(O\).
Gọi \(H\) là trung điểm của \(AB\), khi đó \(H\left( {15;15;0} \right)\), ta có \(OH \bot AB\).
Đường thẳng \(OH\) đi qua \(O\left( {0;0;0} \right)\) và có VTCP \(\overrightarrow {OH} = \left( {15;15;0} \right) = 15\left( {1;1;0} \right)\) là: \(\left\{ \begin{array}{l}x = t\\y = t\\z = 0\end{array} \right.\).
Để \(M \in \left( {OAB} \right)\) thỏa mãn \(MA + MB\) nhỏ nhất thì \(M,A,B\) phải đồng phẳng và \(MA = MB\).
Vì \(MH\) nhỏ nhất. Khi đó \(M\) là giao điểm của \(OH\) và mặt cầu \(\left( S \right)\).
Tọa độ \(M\) thỏa mãn phương trình: \({t^2} + {t^2} + {0^2} = 40,96 \Leftrightarrow 2{t^2} = 40,96 \Leftrightarrow t = \pm \frac{{16\sqrt 2 }}{5}\).
Suy ra \[\left[ \begin{array}{l}{M_1}\left( {\frac{{16\sqrt 2 }}{5};\frac{{16\sqrt 2 }}{5};0} \right) \Rightarrow {M_1}H \approx 14,81\\{M_2}\left( {\frac{{ - 16\sqrt 2 }}{5};\frac{{ - 16\sqrt 2 }}{5};0} \right) \Rightarrow {M_2}H \approx 27,61.\end{array} \right.\]
Vậy điểm cần tìm là: \[M\left( {\frac{{16\sqrt 2 }}{5};\frac{{16\sqrt 2 }}{5};0} \right)\] .
Khi đó, \(T = MA + MB = 2MA = 2\sqrt {{{\left( {\frac{{16\sqrt 2 }}{5} - 30} \right)}^2} + {{\left( {\frac{{16\sqrt 2 }}{5} - 0} \right)}^2} + {0^2}} \approx 51,7\).
Đáp án: 51,7.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
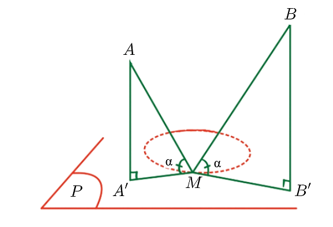
Gọi \(A',B'\) lần lượt là hình chiếu vuông góc của \(A,B\) lên mặt phẳng \(\left( P \right)\).
Góc tạo bởi \(MA\) với mặt vườn và góc tạo bởi \(MB\) với mặt vườn phải luôn bằng nhau.
Nên ta có \( \Rightarrow \frac{{MA}}{{MB}} = \frac{{AA'}}{{BB'}} = \frac{{d\left( {A,\left( P \right)} \right)}}{{d\left( {B,\left( P \right)} \right)}}\).
Mà \(d\left( {A,\left( P \right)} \right) = \frac{{\left| {2 \cdot 40 + 2 \cdot \left( { - 40} \right) - 12 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 8\); \[d\left( {B,\left( P \right)} \right) = \frac{{\left| {2 \cdot \left( { - 40} \right) + 2 \cdot 50 - 38 - 12} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - 1} \right)}^2}} }} = 10\].
\( \Rightarrow \frac{{MA}}{{MB}} = \frac{8}{{10}} = \frac{4}{5} \Rightarrow 5MA = 4MB\). Gọi \(M\left( {x;y;z} \right)\). Khi đó, ta được:
\(25 \cdot \left[ {{{\left( {x - 40} \right)}^2} + {{\left( {y + 40} \right)}^2} + {{\left( {z - 12} \right)}^2}} \right] = 16 \cdot \left[ {{{\left( {x + 40} \right)}^2} + {{\left( {y - 50} \right)}^2} + {{\left( {z - 38} \right)}^2}} \right]\).
Rút gọn ta được phương trình mặt cầu \(\left( S \right)\) chứa các điểm \(M\) thoả mãn yêu cầu kĩ thuật:
\({x^2} + {y^2} + {z^2} - \frac{{3280}}{9}x + 400y + \frac{{616}}{9}z - \frac{{5104}}{9} = 0\).
Đồng thời, vì điểm \(M\) nằm trên mặt vườn nên \(M \in \left( P \right):\;{\mkern 1mu} 2x + 2y - z - 12 = 0\).
Như vậy, tập hợp điểm \(M\) cần tìm là giao tuyến của mặt cầu \(\left( S \right)\) và mặt phẳng \(\left( P \right)\), tức là một đường tròn \(\left( C \right)\).
Gọi \(I\) là tâm mặt cầu \(\left( S \right)\), ta được: \(I\left( {\frac{{1640}}{9}; - 200; - \frac{{308}}{9}} \right)\).
Bán kính của mặt cầu \(\left( S \right)\):
\(R = \sqrt {{a^2} + {b^2} + {c^2} - d} = \sqrt {{{\left( {\frac{{1640}}{9}} \right)}^2} + {{\left( { - 200} \right)}^2} + {{\left( {\frac{{ - 308}}{9}} \right)}^2} + \frac{{5104}}{9}} = \sqrt {\frac{{6070400}}{{81}}} \).
Khoảng cách từ tâm \(I\) đến mặt phẳng \(\left( P \right)\): \(d = \frac{{\left| {2 \cdot \frac{{1640}}{9} + 2 \cdot \left( { - 200} \right) + \frac{{308}}{9} - 12} \right|}}{{\sqrt {4 + 4 + 1} }} = \frac{{40}}{9}\).
Bán kính đường tròn giao tuyến \(\left( C \right)\): \(r = \sqrt {{R^2} - {d^2}} = \sqrt {\frac{{6068800}}{{81}}} \).
Vậy độ dài đường ray là chu vi đường tròn \(\left( C \right)\): \(l = 2\pi r \approx 1720\;{\rm{(m)}}\).
Đáp án: 1720.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \[M = AB \cap CD\] (là điểm hai viên đạn va chạm nhau) khi đó \[AM = 150\,{\rm{m}}\;(1)\].
Ta có \[\overrightarrow {AB} = \left( {1\,;2\,;2} \right)\] là vectơ chỉ phương của đường thẳng \[AB\].
Phương trình tham số đường thẳng \[AB\] là \[\left\{ {\begin{array}{*{20}{c}}{x = 5 + t}\\{y = 7 + 2t}\\{z = 10 + 2t}\end{array}} \right.\quad (t \in \mathbb{R})\].
Do \[M \in AB \Rightarrow M\left( {5 + t;7 + 2t;10 + 2t} \right)\]. Từ (1) ta có \[\sqrt {{t^2} + 4{t^2} + 4{t^2}} = 150 \Leftrightarrow \left| t \right| = 50\].
Với \[t = 50 \Rightarrow M\left( {55;107;110} \right)\] và với \[t = - 50 \Rightarrow M\left( { - 45; - 93; - 90} \right)\].
Vì cao độ điểm \[D\] dương nên cao độ của điểm \[M\] dương\[ \Rightarrow M\left( {55\,;107\,;110} \right)\].
Vậy vectơ chỉ phương của đường thẳng \[CD\] là \[\overrightarrow {CM} = \left( {40;90;105} \right)\].
Khi đó, phương trình tham số đường thẳng \[CD\] là \[\left\{ {\begin{array}{*{20}{c}}{x = 15 + 40t'}\\{y = 17 + 90t'}\\{z = 5 + 105t'}\end{array}} \right.\quad (t' \in \mathbb{R})\].
Mà điểm \[D\] cách mặt đất \[26\,{\rm{m}}\] nên điểm \[D\] có cao độ bằng \[26\]
\[ \Rightarrow \]\[5 + 105t' = 26 \Leftrightarrow t' = \frac{1}{5} \Rightarrow D\left( {23\,;35\,;26} \right)\]. \[C\left( {15\,;17\,;5} \right)\]
Khi đó độ dài \[CD = \sqrt {{{\left( {15 - 23} \right)}^2} + {{\left( {17 - 35} \right)}^2} + {{\left( {5 - 26} \right)}^2}} \approx 28,8\,\,{\rm{(m)}}.\]
Đáp án: 28,8.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập