Sắp xếp các số hữu tỉ \(\frac{{ - 7}}{{20}};\,\frac{5}{{ - 20}};\,\frac{{ - 5}}{{17}};\,\frac{1}{{ - 3}}\) theo thứ tự tăng dần được:

(1,5 điểm) Một cửa hàng điện thoại nhập một chiếc Iphone 14 promax từ Trung Quốc là 27,5 triệu đồng. Khi về Việt Nam, cửa hàng đã bán với giá niêm yết bằng 160% so với giá nhập.

(a) Hỏi giá niêm yết của một chiếc Iphone đó tại cửa hàng là bao nhiêu?

(b) Cửa hàng nhập về một lô hàng 50 chiếc điện thoại Iphone 14 promax với chi phí vận chuyển là 20 triệu đồng. Với 15 chiếc điện thoại đó được bán đầu tiên, khi thanh toán bằng quét mã VNPAY-QR sẽ được giảm 500 nghìn đồng. Hỏi sau khi bán hết lô hàng 50 chiếc Iphone thì cửa hàng lãi bao nhiêu tiền (không tính các chi phí khác ngoài chi phí vận chuyển)?

(2,0 điểm) Cho hình vẽ bên.

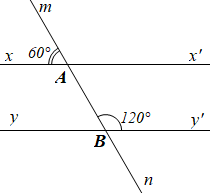
(a) Vẽ lại hình (đúng số đo các góc) và viết giả thiết, kết luận của bài toán.

(b) Tính số đo góc \(\widehat {mAx'}\).

(c) Giải thích tại sao hai tia \(xx'\) và \(yy'\) song song.

(d) Vẽ tia \(Aa\) là tia phân giác của \(\widehat {xAn}\) và tia \(Bb\) nằm trong \(\widehat {mBy'}\) song song với tia \[Aa\]. Chứng minh tia \(Bb\) là tia phân giác của \(\widehat {mBy'}.\)

(0,5 điểm) Tìm các số nguyên \(a,\,b\) thỏa mãn \(a\left( {\sqrt 5 - 1} \right) + b\left( {\sqrt 5 + 1} \right) = 2\).

Số \(37,7536\) được làm tròn thành \(37,75\). Độ chính xác của phép làm tròn là

Qua điểm \(A\) nằm ngoài đường thẳng \(a\), ta vẽ hai đường thẳng song song với \(a\) thì

Cho ba đường thẳng \(a,\,\,b,\,\,c\) phân biệt. Nếu \(a \bot c\) và \(c \bot b\) thì

(2,0 điểm) Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):

(a) \(\frac{2}{5} - \frac{1}{5}.\frac{3}{{ - 4}}\)

(b) \(\frac{{{5^4}{{.20}^4}}}{{{{25}^5}{{.4}^5}}}\)

(c) \(\sqrt {\frac{4}{9}} - \left| {\frac{{ - 3}}{7}} \right|.\frac{7}{8}\)

(d) \(\left( {\frac{{ - 3}}{4} + \frac{4}{{15}}} \right):\frac{{2022}}{{2023}} + \left( {\frac{{ - 1}}{4} + \frac{{11}}{{15}}} \right):\frac{{2022}}{{2023}}\).