Cho trục số bên.
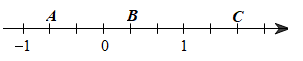
Khẳng định nào sau đây là đúng?
Điểm \(A\) biểu diễn số \(\frac{{ - 1}}{3}\)
Điểm \(B\) biểu diễn số \(\frac{1}{3}\)
Điểm \(C\) biểu diễn số \(\frac{4}{3}\)
Điểm \(A\) biểu diễn số \(\frac{{ - 3}}{2}\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: B
Quan sát trục số ta thấy:
‒ Điểm \(A\) biểu diễn số \(\frac{{ - 2}}{3}\);
‒ Điểm \(B\) biểu diễn số \(\frac{1}{3}\);
‒ Điểm \(C\) biểu diễn số \(\frac{5}{3}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

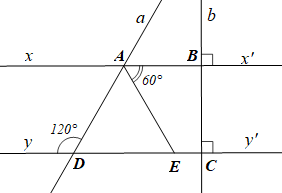
b) Do \(b \bot xx'\) và \(b \bot yy'\) nên \[xx'{\rm{ // }}yy'\] (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau).
c) Do \[xx'{\rm{ // }}yy'\] (câu a) nên \(\widehat {BAD} = \widehat {ADy}\) (hai góc so le trong)
Mà \(\widehat {ADy} = 120^\circ \) (giả thiết) nên \[\widehat {BAD} = 120^\circ \].
d) Ta có \(\widehat {BAE} + \widehat {DAE} = \widehat {BAD}\) (hai góc kề nhau)
\(60^\circ + \widehat {DAE} = 120^\circ \)
\(\widehat {DAE} = 120^\circ - 60^\circ = 60^\circ \)
Do đó \(\widehat {BAE} = \widehat {DAE}\) (cùng bằng \(60^\circ \))
Lại có tia \[AE\] nằm giữa hai tia \[AB\] và \[AD\] nên tia \[AE\] là tia phân giác của \(\widehat {BAD}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\[1,93\]
\[1,928\]
\[1,9284\]
\[1,9\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.