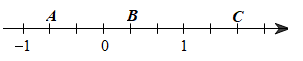(2,0 điểm) Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
(a) \(\frac{7}{4} - \frac{3}{4}:\frac{{ - 1}}{3}\)
(b) \(\left( {{{15}^5}:{5^5}} \right).\left( {{3^5}:{6^5}} \right)\)
(c) \(\sqrt {\frac{{49}}{{81}}} - \left| {\frac{{ - 7}}{3}} \right|\)
(d) \(\frac{1}{9}.\frac{2}{7} + \frac{1}{9}:\frac{7}{5} + \frac{{{{\left( { - 1} \right)}^0}}}{7}\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
a) \(\frac{7}{4} - \frac{3}{4}:\frac{{ - 1}}{3} = \frac{7}{4} - \frac{3}{4}.\frac{3}{{ - 1}} = \frac{7}{4} + \frac{9}{4} = 4\);
b) \[\left( {{{15}^5}:{5^5}} \right).\left( {{3^5}:{6^5}} \right) = {\left( {15:3} \right)^5}.{\left( {3:6} \right)^5} = {5^5}:{\left( {\frac{1}{2}} \right)^5} = {\left( {5:\frac{1}{2}} \right)^5} = {10^5} = 100\,\,000\];
c) \(\sqrt {\frac{{49}}{{81}}} - \left| {\frac{{ - 7}}{3}} \right| = \frac{7}{9} - \frac{7}{3} = \frac{{21}}{{27}} - \frac{{63}}{{27}} = \frac{{ - 42}}{{27}} = - \frac{{14}}{9}\);
d) \(\frac{1}{9}.\frac{2}{7} + \frac{1}{9}:\frac{7}{5} + \frac{{{{\left( { - 1} \right)}^0}}}{7} = \frac{1}{9}.\frac{2}{7} + \frac{1}{9}.\frac{5}{7} + \frac{1}{7} = \frac{1}{9}.\left( {\frac{2}{7} + \frac{5}{7}} \right) + \frac{1}{7} = \frac{1}{9}.1 + \frac{1}{7} = \frac{7}{{63}} + \frac{9}{{63}} = \frac{{16}}{{63}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

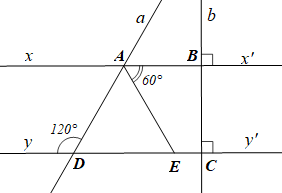
b) Do \(b \bot xx'\) và \(b \bot yy'\) nên \[xx'{\rm{ // }}yy'\] (hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì song song với nhau).
c) Do \[xx'{\rm{ // }}yy'\] (câu a) nên \(\widehat {BAD} = \widehat {ADy}\) (hai góc so le trong)
Mà \(\widehat {ADy} = 120^\circ \) (giả thiết) nên \[\widehat {BAD} = 120^\circ \].
d) Ta có \(\widehat {BAE} + \widehat {DAE} = \widehat {BAD}\) (hai góc kề nhau)
\(60^\circ + \widehat {DAE} = 120^\circ \)
\(\widehat {DAE} = 120^\circ - 60^\circ = 60^\circ \)
Do đó \(\widehat {BAE} = \widehat {DAE}\) (cùng bằng \(60^\circ \))
Lại có tia \[AE\] nằm giữa hai tia \[AB\] và \[AD\] nên tia \[AE\] là tia phân giác của \(\widehat {BAD}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
\[1,93\]
\[1,928\]
\[1,9284\]
\[1,9\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Điểm \(A\) biểu diễn số \(\frac{{ - 1}}{3}\)
Điểm \(B\) biểu diễn số \(\frac{1}{3}\)
Điểm \(C\) biểu diễn số \(\frac{4}{3}\)
Điểm \(A\) biểu diễn số \(\frac{{ - 3}}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.