Cho \(\Delta ABC\) có \(AB = AC = 12\;{\rm{cm}}{\rm{.}}\) Tia phân giác của góc \(B\) cắt đường cao \(AH\;\left( {H \in BC} \right)\) của \(\Delta ABC\) tại \(I.\) Biết rằng \(\frac{{AI}}{{AH}} = \frac{3}{5}.\) Tính chu vi \(\Delta ABC.\) (Đơn vị: \({\rm{cm}}\)).
Cho \(\Delta ABC\) có \(AB = AC = 12\;{\rm{cm}}{\rm{.}}\) Tia phân giác của góc \(B\) cắt đường cao \(AH\;\left( {H \in BC} \right)\) của \(\Delta ABC\) tại \(I.\) Biết rằng \(\frac{{AI}}{{AH}} = \frac{3}{5}.\) Tính chu vi \(\Delta ABC.\) (Đơn vị: \({\rm{cm}}\)).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(40\)
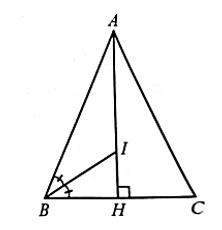
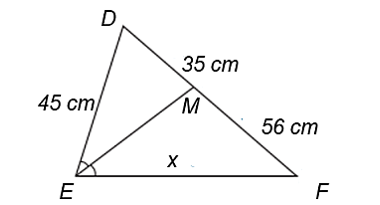
Vì \(\frac{{AI}}{{AH}} = \frac{3}{5}\) nên \(\frac{{AI}}{{IH}} = \frac{3}{2}.\)
Vì \(BI\) là tia phân giác của \(\widehat {ABH}\) trong \(\Delta AHB\) nên \(\frac{{AB}}{{BH}} = \frac{{AI}}{{IH}} = \frac{3}{2}.\)
Do đó, \(BH = \frac{2}{3}AB = \frac{2}{3} \cdot 12 = 8\;\left( {{\rm{cm}}} \right).\)
Vì \(AB = AC = 12\;{\rm{cm}}\) nên \(\Delta ABC\) cân tại \(A.\)
Nên \(AH\) là đường cao đồng thời là đường trung tuyến của tam giác đó.
Suy ra: \(BC = 2BH = 2 \cdot 8 = 16\;\left( {{\rm{cm}}} \right).\)
Chu vi \(\Delta ABC\) là: \(AB + AC + BC = 12 + 12 + 16 = 40\;\left( {{\rm{cm}}} \right).\)
Vậy chu vi \(\Delta ABC\) bằng \(40\;{\rm{cm}}{\rm{.}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(x = 62\;{\rm{cm}}.\)
B. \(x = 72\;{\rm{cm}}.\)
C. \(x = 70\;{\rm{cm}}.\)
D. \(x = 60\;{\rm{cm}}.\)
Câu 2
A. \(BC = 20\;{\rm{cm}}{\rm{.}}\)
B. \(BC = 20,4\;{\rm{cm}}{\rm{.}}\)
C. \(BC = 20,8\;{\rm{cm}}{\rm{.}}\)
D. \(BC = 20,6\;{\rm{cm}}{\rm{.}}\)
Lời giải
Đáp án đúng là: C
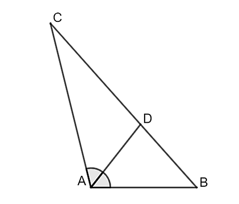
Vì \(AD\) là đường phân giác của \(\Delta ABC\) nên \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}.\) Suy ra: \(DC = \frac{{AC \cdot BD}}{{AB}} = \frac{{16 \cdot 8}}{{10}} = 12,8\;\left( {{\rm{cm}}} \right).\)
Do đó, \(BC = CD + DB = 12,8 + 8 = 20,8\;\left( {{\rm{cm}}} \right).\) Vậy \(BC = 20,8\;{\rm{cm}}{\rm{.}}\)
Câu 3
A. \(\widehat {DAC} = 60^\circ .\)
B. \(\widehat {DAC} = 40^\circ .\)
C. \(\widehat {DAC} = 50^\circ .\)
D. \(\widehat {DAC} = 45^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\widehat {ABD} = \frac{2}{3}\widehat {DBC}.\)
B. \(\widehat {ABD} = \frac{4}{5}\widehat {DBC}.\)
C. \(\widehat {ABD} = \frac{3}{4}\widehat {DBC}.\)
D. \(\widehat {ABD} = \widehat {DBC}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
a) \(\frac{{CM}}{{CB}} = \frac{1}{2}.\)
Đúng
Sai
b) \(BE = 2EM.\)
Đúng
Sai
c) Thời gian bạn Dũng đi gấp hai lần thời gian bạn Minh đi khi hai bạn gặp nhau tại điểm \(E.\)
Đúng
Sai
d) Bạn Dũng cần xuất phát lúc \(12\) giờ thì hai bạn gặp nhau tại điểm \(E\) lúc \(13\) giờ \(30\) phút.
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\frac{{AB}}{{AC}} = \frac{{BD}}{{DC}}.\)
B. \(\frac{{AB}}{{AC}} = \frac{{DC}}{{DB}}.\)
C. \(\frac{{AB}}{{AC}} = \frac{{BD}}{{BC}}.\)
D. \(\frac{{AB}}{{AC}} = \frac{{DC}}{{BC}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập