Điểm nào dưới đây thuộc đồ thị của hàm số bậc nhất \(y = - 6x + 5?\)
Quảng cáo
Trả lời:
Đáp án đúng là: B
Với \(x = 0\) ta có: \(y = \left( { - 6} \right) \cdot 0 + 5 = 5.\) Vậy điểm \(B\left( {0;\;\,5} \right)\) thuộc đồ thị của hàm số \(y = - 6x + 5.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \( - 2,5\)
Để \(y = \left( {m - 1} \right)x - 3m\) là hàm số bậc nhất thì \(m - 1 \ne 0,\) suy ra \(m \ne 1.\)
Vì đồ thị hàm số \(y = \left( {m - 1} \right)x - 3m\) đi qua điểm \(N\left( {1;\;\,4} \right)\) nên \(4 = \left( {m - 1} \right) \cdot 1 - 3m,\) suy ra \(m = - 2,5\) (thỏa mãn). Vậy với \(m = - 2,5\) thì đồ thị hàm số \(y = \left( {m - 1} \right)x - 3m\) đi qua điểm \(N\left( {1;\;\,4} \right).\)
Câu 2
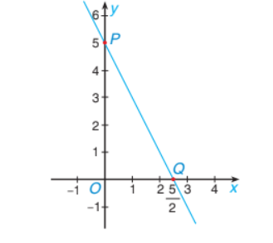
a) Đồ thị hàm số \(y = f\left( x \right)\) là đồ thị hàm số bậc nhất.
Lời giải
a) Đúng.
Đồ thị hàm số \(y = f\left( x \right)\) là một đường thẳng nên đồ thị hàm số \(y = f\left( x \right)\) là đồ thị hàm số bậc nhất.
b) Sai.
Đồ thị hàm số \(y = f\left( x \right)\) đi qua hai điểm \(P\left( {0;\;\,5} \right)\) và \(Q\left( {\frac{5}{2};\;\,0} \right).\)
c) Đúng.
Đồ thị hàm số \(y = f\left( x \right)\) là đồ thị hàm số bậc nhất nên đồ thị hàm số có dạng \(y = ax + b\;\,\left( {a \ne 0} \right).\)
Vì đồ thị hàm số \(y = ax + b\) đi qua điểm \(P\left( {0;\;\,5} \right)\) nên \(5 = a \cdot 0 + b,\) suy ra \(b = 5.\) Khi đó, \(y = ax + 5.\)
Vì đồ thị hàm số \(y = ax + 5\) đi qua điểm \(Q\left( {\frac{5}{2};\;\,0} \right)\) nên \(0 = \frac{5}{2}a + 5,\) suy ra \(a = - 2\) (thỏa mãn).
Vậy đồ thị hàm số trên là \(y = - 2x + 5.\)
d) Sai.
Với \(x = 1\) thay vào \(y = - 2x + 5\) ta có: \(y = \left( { - 2} \right) \cdot 1 + 5 = 3.\)
Vậy \(M\) có hoành độ bằng 1 thuộc đồ thị hàm số \(y = f\left( x \right)\) thì tung độ bằng 3.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.