Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất \(y = ax + b,\) trong đó \(b\) biểu thị chi phí cố định của hoạt động kinh doanh và \(a\) biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 30 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là \(1,5\) triệu đồng. Gọi \(y\) (triệu đồng) là chi phí để sản xuất \(x\) xe đạp trong một ngày.
Hàm chi phí đơn giản nhất là hàm chi phí bậc nhất \(y = ax + b,\) trong đó \(b\) biểu thị chi phí cố định của hoạt động kinh doanh và \(a\) biểu thị chi phí của mỗi mặt hàng được sản xuất. Giả sử rằng một xưởng sản xuất xe đạp có chi phí cố định hằng ngày là 30 triệu đồng và mỗi chiếc xe đạp có chi phí sản xuất là \(1,5\) triệu đồng. Gọi \(y\) (triệu đồng) là chi phí để sản xuất \(x\) xe đạp trong một ngày.
Quảng cáo
Trả lời:
a) Sai.
Theo đầu bài ta có: \(y = 30 + 1,5x\) (triệu đồng).
b) Đúng.
Vì hàm số bậc nhất có dạng \(y = ax + b\;\,\left( {a \ne 0} \right)\) nên hàm số \(y = 30 + 1,5x\) là hàm số bậc nhất.
c) Sai.
Với \(x = 10\) ta có: \(y = 30 + 1,5x = 30 + 1,5 \cdot 10 = 45\) (triệu đồng).
Vậy chi phí sản xuất 10 chiếc xe trong một ngày nhỏ hơn 50 triệu đồng.
d) Đúng.
Với \(y = 220\) ta có: \(220 = 30 + 1,5x\) nên \(x = \frac{{380}}{3} \approx 126,67.\)
Vậy với chi phí trong một ngày là 220 triệu đồng thì có thể sản xuất được nhiều hơn 100 xeHot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \( - 2,5\)
Để \(y = \left( {m - 1} \right)x - 3m\) là hàm số bậc nhất thì \(m - 1 \ne 0,\) suy ra \(m \ne 1.\)
Vì đồ thị hàm số \(y = \left( {m - 1} \right)x - 3m\) đi qua điểm \(N\left( {1;\;\,4} \right)\) nên \(4 = \left( {m - 1} \right) \cdot 1 - 3m,\) suy ra \(m = - 2,5\) (thỏa mãn). Vậy với \(m = - 2,5\) thì đồ thị hàm số \(y = \left( {m - 1} \right)x - 3m\) đi qua điểm \(N\left( {1;\;\,4} \right).\)
Câu 2
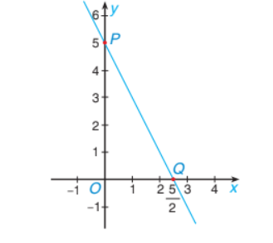
a) Đồ thị hàm số \(y = f\left( x \right)\) là đồ thị hàm số bậc nhất.
Lời giải
a) Đúng.
Đồ thị hàm số \(y = f\left( x \right)\) là một đường thẳng nên đồ thị hàm số \(y = f\left( x \right)\) là đồ thị hàm số bậc nhất.
b) Sai.
Đồ thị hàm số \(y = f\left( x \right)\) đi qua hai điểm \(P\left( {0;\;\,5} \right)\) và \(Q\left( {\frac{5}{2};\;\,0} \right).\)
c) Đúng.
Đồ thị hàm số \(y = f\left( x \right)\) là đồ thị hàm số bậc nhất nên đồ thị hàm số có dạng \(y = ax + b\;\,\left( {a \ne 0} \right).\)
Vì đồ thị hàm số \(y = ax + b\) đi qua điểm \(P\left( {0;\;\,5} \right)\) nên \(5 = a \cdot 0 + b,\) suy ra \(b = 5.\) Khi đó, \(y = ax + 5.\)
Vì đồ thị hàm số \(y = ax + 5\) đi qua điểm \(Q\left( {\frac{5}{2};\;\,0} \right)\) nên \(0 = \frac{5}{2}a + 5,\) suy ra \(a = - 2\) (thỏa mãn).
Vậy đồ thị hàm số trên là \(y = - 2x + 5.\)
d) Sai.
Với \(x = 1\) thay vào \(y = - 2x + 5\) ta có: \(y = \left( { - 2} \right) \cdot 1 + 5 = 3.\)
Vậy \(M\) có hoành độ bằng 1 thuộc đồ thị hàm số \(y = f\left( x \right)\) thì tung độ bằng 3.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.